7.2. Markov Localization
probabilistic localization algorithms는 Bayes filter의 변형입니다. localization problem을 위한 직관적인 bayes filter의 응용은 Markov Localization이라고 합니다. 그림 7.1.은 그 기본적인 알고리즘을 보여줍니다.


이 알고리즘은 Bayes_filter로부터 나왔습니다. 차이점은 입력으로 $m$을 필요로 한다는 점입니다. 여기서 map은 line 4의 measurement model $p(z_t | x_t, m)$에서 사용됩니다. 항상은 아니지만, 종종, line 3에서 motion model $p(x_t | u_t, x_{t-1}, m)$에서도 사용됩니다. Bayes filer처럼, markov localization은 시간 $t-1$에서의 probabilistic belief를 $t$에서의 belief로 transform합니다. markov localization은 global localization problem, prosition tracking problem, 통계적 환경에서의 kidnapped robot problem에서 사용됩니다.
초기의 belief $bel(x_0)$은 초기 로봇 pose에 대한 정보를 나타냅니다. 이는 localization problem의 종류에 따라 다르게 정합니다.
Position tracking
만약 초기 pose를 알고있으면, $bel(x_0)$은 확률 질량 분포로 초기화됩니다. $\overline {x} _0$을 우리가 알고있는 초기의 pose라고 하겠습니다. 즉,

확률 질량 분포는 불연속적이므로 밀도를 갖지 않습니다.
실제로 초기 pose는 보통 approximation으로 구합니다. $bel(x_0)$은 보통 중심이 $\overline {x} _0$인 좁은 형태의 Gaussian 분포로 초기화됩니다. 여기서 $\Sigma$는 초기 pose uncertainty의 공분산입니다.

Global localization
만약 초기 pose를 모른다면, $bel(x_0)$은 map 전체에서 가능한 모든 공간에 uniform distribution됩니다.
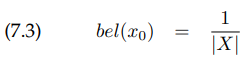
여기서 $|X|$는 map 내에서 가능한 모든 pose의 공간의 부피(Lebesgue measure)입니다.
Other
로봇의 위치에 대해 일부 아는 것은 적절한 초기 분포로 transform될 수 있습니다. 예를 들어, 만약 로봇이 문 옆에서 출발한다고 했을 때, 우리는 $bel(x_0)$을 문 근처를 uniform distribution하고, 그 부분을 제외한 나머지 위치를 다 0으로 초기화할 수 있습니다. 만약 어떤 특정 복도에 위치한다고 하면, 그 복도를 제외한 나머지 영역을 0으로 초기화 할 수 있습니다.
3. Illustration of Markov Localization
그림 7.5.는 3개의 다른 문이 있는, 1차원 복도에서의 예제를 나타냅니다.

그림 7.5. (a)에서는 $bel(x_0)$은 로봇이 위치할 수 있는 모든 위치에 분포된 uniform density를 볼 수 있습니다. 로봇이 센서를 통해 감지하고, 문 옆에 있다는 것을 알게되면서 로봇은 알고리즘의 line 4와 같이 $bel(x_0)$을 $p(z_t | x_t, m)$과 곱합니다. 7.5 (b)에서의 위쪽 그래프는 $p(z_t | x_t, m)$을 보여줍니다. 로봇이 문 옆에 있다는 것은 아는데 어떤 문인지 모르니 저렇게 3개의 문에 비슷한 가우시안 분포를 가지는 그래프를 보입니다. 즉, 이 결과는 multi-modal 형태인데, 이는 이 지점에서의 로봇의 residual uncertainty를 반영하는 것을 보여줍니다.
로봇이 오른쪽으로 움직이면, 7.5 (c)와 처럼 됩니다. 이는 motion model을 포함한 $p(x_t | u_t, x_{t-1})$을 계산한 belief를 나타냅니다. 이 motion model은 하나의 pose에 집중하는 것이 아니라 noise-free motion일 경우에 어떻게 움직였을지에 대한 기대값 만큼 전체적으로 pose들을 이동한것이며, noise로 인해 전체적으로 Gaussian 모양의 그래프들의 분산이 조금 커진것을 볼 수 있습니다.
마지막 측정은 7.5 (d)인데, 현재의 belief를 perceptual probability $p(z_t | x_t)$와 곱하는 것을 보여줍니다. 즉, 7.5 (d)에서의 측정값 $p(z|x)$를 7.5 (c)에서의 belief와 곱하는 것입니다. 여기서, 대부분의 확률 질량 함수는 올바른 pose에 집중되게 되며, 로봇이 이제는 꽤나 자신의 위치에 대한 확신을 갖게됩니다. 7.5. (e)는 로봇이 다시 움직이면서 전체적으로 분산이 커지는 것을 보여줍니다.