2-3. Robot Environment Interaction
이 글은 Sebastian thrun의 Probabilistic Robotics를 보고 내용을 정리한 글이며, 나름 쉽게 표현하기 위해서 의역을 한 부분이 있습니다.
1. 상태(State)
환경(Environment) 은 상태(state)에 의해 나타내어집니다. 즉, 이렇게 생각하면 됩니다. 상태란, 미래(future)에 영향을 줄 수 있는 로봇과 그 환경의 모든 양상(aspect)입니다.
몇몇 상태 변수(variable)는 시간에 따라 바뀌는데, 예를 들면 로봇 근처의 사람이라든지 뭐 이런 걸 생각하시면 됩니다. 반면, 변하지 않고 정적인(static) 상태가 있는데, 예를 들면 벽이나 건물 같은 이런 것을 말합니다.
이렇게 바뀌는 상태를 동적 상태(dynamic state)라고 하고, 바뀌지 않는 상태를 정적 상태(static state)라고 합니다. 상태는 센서가 제대로 작동하든 말든 로봇의 자세(pose), 속도(velocity) 같은 로봇 자체에 관련된 변수들 또한 포함합니다.
이제 우리는 상태를 $x$라고 하고, 시간 $t$에서의 상태를 $x_t$라고 합니다.
만약 상태 $x_t$가 미래를 예측하기 가장 좋은 값이라고 한다면, 상태 $x_t$는 complete라고 합니다. completeness란, 과거의 상태, 측정, 또는 컨트롤이 미래에 대한 예측을 정확하게 하는데 더 이상의 도움을 주지 못하는 것을 의미합니다. 즉, 미래는 확률적이지만, 만약 이 의존성이 상태 $x_t$에 의해 영향을 받지 않았다면 $x_t$ 전의 어떤 변수도 확률적으로 더 개선된 값을 줄 수 없다는 것입니다.
2. 환경 상호작용(Environment Interaction)
로봇과 로봇의 환경 간에는 두 종류의 근본적인(fundamental) 상호작용이 있습니다.
그 상호작용이란, 로봇은 로봇의 액추에이터(actuator)를 통해 그 환경에 영향을 줄 수 있고, 센서를 통해 상태에 대한 정보를 얻을 수 있다는 것입니다.
그 두 종류의 상호작용은 동시에 발생할(co-occur) 수 있지만, 지금까지 경험해본 바에 의하면 그 둘을 따로 분리해서 생각하는 것이 좋습니다
- 환경 센서 측정(Envrionment sensor measurement)
인식(perception)은 로봇이 주변 환경의 정보를 획득하기 위해 센서를 사용하는 과정(process)입니다. 예를 들면 카메라로 이미지를 얻고, 거리 측정이나 촉각 센서 등으로 주변 환경의 정보를 획득하는 것입니다.
이러한 인식의(perceptual) 상호작용은 측정(meaesurement)라고 불리며, 가끔 우리는 이것을 관측(observation)이나 인식(percept)라고 합니다.
일반적으로, 센서 측정은 약간의 딜레이가 있습니다. 그러므로 센서는 잠깐 이전의 상태에 대한 정보를 제공하는 것입니다.
- 컨트롤 액션(Control action)
컨트롤 액션은 월드(world)의 상태를 바꿉니다. 즉, 능동적(actively)으로 로봇의 환경에 힘을 가하는 것으로 환경을 바꾼다는 것입니다. 예를 들면 로봇의 움직임이나 물체를 다루는(manipulate) 것을 말합니다. 심지어 로봇이 아무 액션을 취하지 않는다고 해도, 일반적으로 상태는 변화합니다. 따라서 우리는 로봇이 심지어 아무 모터를 움직이지 않는다거나 해도 항상 컨트롤 액션을 실행한다고 가정합니다. 실제로, 로봇은 계속해서 컨트롤과 측정을 수행합니다.
우리는 여기서 로봇은 과거의 센서 측정과 컨트롤 액션을 기록한다고 가정하고, 이러한 수집(collection)을 데이터(data)라고 합니다(이 데이터가 계속 기억(memorize) 되든 않든 상관없습니다).
- 환경 측정 데이터(Envrionment measurement data)
환경 측정 데이터는 잠깐의 환경 상태에 대한 정보를 제공합니다. 예를 들면 카메라 이미지나 거리 측정 같은 이런 것을 말합니다. 대부분의 경우, 우리는 타이밍 효과(timing effect)를 무시합니다(예를 들어, LIDAR같은 레이저 센서의 경우 환경을 센서가 회전하면서 순차적으로(sequentially) 매우 빠르게 스캔하지만, 우리는 이것을 같은 시간에 측정된 데이터라고 가정합니다.) 이렇게 시간 $t$에 측정된 데이터를 $z_t$라고 할 것입니다. 또한, 우리는 편의상 하나의 시간에 하나의 측정만을 한다고 가정할 것입니다. 시간 $t_1$에서 $t_2$까지 측정된 데이터는 다음과 같이 나타냅니다.
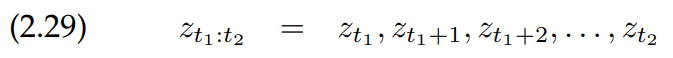
- 컨트롤 데이터(Control data)
컨트롤 데이터는 환경에서의 상태의 변화에 대한 정보를 담고 있습니다. 예를 들어, 로보틱스에서 컨트롤 데이터에 대한 일반적인 예는 로봇의 속도입니다. 로봇의 속도를 10cm/sec로 설정하고 5초간 이 명령을 수행하면 로봇의 자세(pose)는 명령 수행 이전에 비해 약 50cm 정도 전진했을 것입니다. 따라서, 컨트롤은 상태의 변화에 관한 정보를 담고 있습니다.
컨트롤 데이터에 대한 대안(alternative source)으로는 오도미터(odometers)가 있습니다. 오도미터는 로봇의 바퀴의 회전을 측정하는 센서인데, 이것은 컨트롤 액션의 효과를 측정하기 때문에 비록 오도미터가 센서라고 할지라도 이것을 컨트롤 데이터처럼 다룰 것입니다.
컨트롤 데이터는 $u_t$라고 나타낼 것이고, 이 변수 $u_t$는 항상 구간 $\left(t-1;t\right]$에서의 상태의 변화에 대응됩니다. 식 2.29에서 나타낸 것처럼, $u_t$도 다음과 같이 나타냅니다.
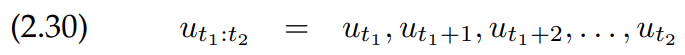
환경은 로봇이 특정한 컨트롤 액션을 실행하지 않는다고 해도 바뀔 수 있기 때문에, 엄밀히 말해서 시간이 흘러간다는 사실은 컨트롤 정보(control information)입니다. 따라서 우리는 "아무것도 하지 않음"이라는 액션을 포함해서 샘플 시간 t에는 하나의 컨트롤 데이터만 존재한다고 가정합니다.
환경 인식은 환경에 대한 정보를 제공하기 때문에 로봇의 지식(knowledge)을 증가시키는 경향이 있습니다. 반면, 움직임(motion)은 로봇의 작동과 로봇 환경의 확률성(stochasticity)에 내재하는(inherent) 노이즈로 인해 로봇의 지식을 감소시키는 경향이 있습니다.
3. 확률적 생성 법칙(Probailistic Generative Laws)
상태와 측정의 변화(evolution)는 확률적 법칙에 의해 통제됩니다(governed) 일반적으로, 상태 $x_t$는 상태 $x_{t-1}$에 의해 확률적으로 만들어집니다. 그러므로, 우리는 $x_t$가 만들어진 것으로부터 확률 분포를 명시(specify) 할 수 있어야 합니다. 처음 보면, 상태 $x_t$는 과거의 상태, 측정, 컨트롤을 조건부로 하는 것으로 보입니다. 따라서, 확률 분포에 의해 나타내어진 상태의 개선을 특징짓는(characterize) 확률적 법칙은 다음과 같은 식으로 주어집니다.
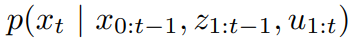
여기서 주목해야 할 것은 로봇은 컨트롤 액션 $u$를 먼저 실행하고, 그다음 측정 $z$를 가진다는 것입니다.
만약 여기서 $x_t$가 그 이전까지 있던 모든 상태에 대한 충분한 정보를 가지고 있다면, $x_{t-1}$또한 그 시간까지 모든 정보를 가지고 있을 것이고, 이 말은 $u_{1:t-1}$와 $z_{1:t-1}$를 포함한 모든 정보를 알기 때문에, 만약 우리가 $x_{t-1}$을 알고 있다고 하면, $u_t$만 알아도 $x_t$를 구할 수 있습니다. 즉, 다음과 같이 나타낼 수 있습니다.
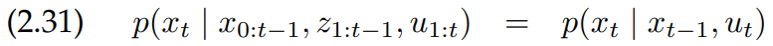
이 식은 조건부 독립의 예를 보여줍니다. 즉, 조건 값들을 알면 몇 변수들은 독립이라는 것입니다. 여기서, 상태에 대한 식이 아닌 측정에 대한 식은 다음과 같이 조건부 독립으로 구할 수 있습니다.
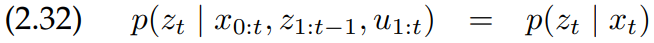
다시 말해, 상태 $x_t$는 측정 $z_t$를 예측하기에 충분하다는 것입니다. 과거의 측정이나 컨트롤, 심지어 상태에 대한 변수에 대해 아는 것은 $x_t$가 complete 하다는 것과 관련이 없습니다.
식 2.31은 상태 과도 확률(state transition probability)라고 하며, 이것은 로봇 컨트롤 $u_t$의 함수로써 시간에 따라 어떻게 상태가 개선되는지를 나타냅니다. 즉, 로봇 환경은 결정적(deterministc)으로 주어지는 것이 아니라 확률적으로 주어진다는 것입니다. 때때로 상태 과도 분포 (state transition distribution)는 시간 $t$에 의존하지 않으며, 이 경우에는 다음과 같이 나타냅니다(위 식과 다르게 밑 첨자에 $t$가 없습니다).
$$p(x' | u, x)$$
여기서 $x'$은 successor(계승자, 이후 모델)라고 하고, $x$는 predecessor(전임자, 이전 모델) state라고 합니다.
식 2.32는 측정 확률(measurement probability)라고 합니다. 이 식 또한 시간 $t$에 의존하지 않을 수 있으며, 이 경우에는 다음과 같이 나타냅니다.
$$p(z | x)$$
상태 과도 확률과 측정 확률은 로봇과 그 환경의 동적 확률 시스템(dynamic stochastic system)을 묘사합니다. 다음 그림은 상태와 측정이 어떻게 개선되는지를 보여줍니다.
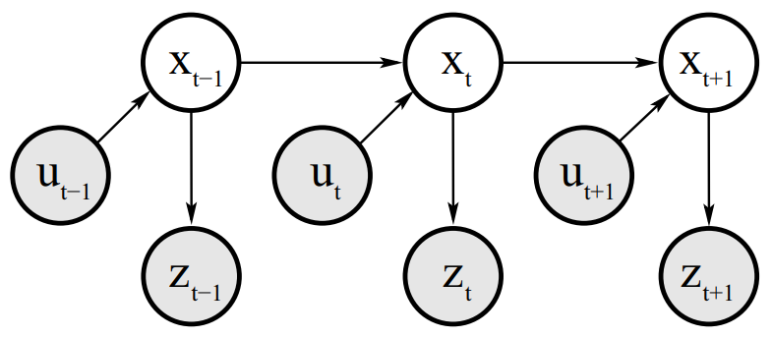
시간 $t$에서의 상태는 확률적으로 시간 $t-1$의 상태와 컨트롤 $u_t$에 의존하며, 측정 $z_t$는 확률적으로 시간 $t$의 상태에 의존합니다.
4. Belief 분포(Belief Distributions)
확률적 로보틱스에 대한 또 다른 중요한 컨셉은 belief에 대한 것입니다. belief는 로봇이 환경에 대한 지식을 얼마나 가지고 있는지를 나타냅니다. 예를 들어, 로봇의 자세가 글로벌 좌표 시스템(global coordinate system)에서 $x_t = \langle14.12, 12.7, 45^\circ\rangle$라고 해도, 일반적으로 자세는 직접적으로 측정될 수 없기 때문에 이 로봇의 자세를 알 수 없습니다. 대신, 로봇은 자신의 자세를 데이터로부터 추론합니다. 따라서 우리는 로봇의 상태에 대한 내부의 belief와 "진짜 상태(true state)"를 구분합니다.
belief 분포는 확률(또는 확률 밀도)를 각각의 진짜 상태에 관한 가능한 확률 값으로 할당합니다. belief 분포는 다음과 같이 가능한 데이터를 조건으로 하는 상태에 대한 사후 확률(posterior)로 나타낼 수 있습니다.
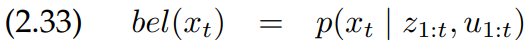
이 사후 확률은 시간 $t$에서의 상태 $x_t$에 대한 확률 분포이며, 과거의 모든 측정 $z_{1:t}$와 모든 컨트롤 $u_{1:t}$를 조건으로 합니다. 앞에서 언급한 것과 비슷하게, belief는 시간 $t$에서의 측정 $z_t$를 포함하는 경우와 포함하지 않은 경우로 나눌 수 있습니다. 즉, $u_t$까지만 실행하고 측정은 아직 하지 않은 경우와 측정을 하고 난 후의 경우입니다. 위 식 2.33은 측정을 포함한 경우이며, 측정을 포함하지 않은 경우는 다음과 같이 나타냅니다.
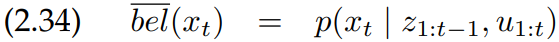
따라서, 식 2.34는 이전 상태의 사후확률을 기반으로 식 2.33을 예측한다는 것입니다. 이렇게 식 2.34를 통해 식 2.33을 계산하는 것을 수정(correction) 또는 측정 업데이트(measurement update)라고 합니다.
위 식 (2.33)과 (2.34)는 앞으로 나올 확률 기반의 로봇의 위치 추정에 대한 기본 식이 되니 꼭 기억해 두세요