[Do it!] 4. 2개의 층 연결하기 - 다층 신경망
이 포스트는 Do it! 정직하게 코딩하며 배우는 딥러닝 입문 pp.160~194를 참고하였습니다.
신경망 알고리즘 계산을 벡터화 하기
기본적인 선형대수 대한 개념은 알고있다는 하에 진행하겠습니다.
SingleLayer 클래스에 배치 경사 하강법 적용하기
이전 포스트에서 사용했던 위스콘신 유방암 데이터 세트와 SingleLayer 클래스를 사용할 것입니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
x = cancer.data
y = cancer.target
x_train_all, x_test, y_train_all, y_test = train_test_split(x, y, stratify=y, test_size=0.2, random_state=42)
x_train, x_val, y_train, y_val = train_test_split(x_train_all, y_train_all, stratify=y_train_all, test_size=0.2, random_state=42)
시작하기 전에, 데이터 세트의 크기를 확인해봅니다.

참고로, 넘파이를 사용하면 행렬 계산 시 절편을 더할 때, 데이터 세트의 크기에 맞춰 (364, 1) 크기의 행렬을 만들 필요가 없습니다. 스칼라를 더할 시, 모든 데이터에 같은 스칼라가 자동으로 더해집니다. 괄호가 있는 윗첨자는 샘플의 번호, 밑 첨자는 특성의 번호입니다.

그래이디언트 계산 이해하기
경사 하강법에서 그래이디언트는 오차와 입력 데이터의 곱이었습니다. 행렬 곱으로 그래이디언트를 계산하는 법은 다음과 같이 표현합니다.

오차는 각 샘플마다 존재하므로 샘플 수와 같은 개수의 오차가 존재하며, 입력값을 전치해서 오차에 곱해줘야합니다. 그래이디언트는 가중치의 개수만큼 존재하므로, 특성의 개수와 같습니다. 그리고, 위의 수식에서 나온 그래이디언트는 모든 샘플들의 그래이디언트의 합입니다. 따라서 그래디언트를 업데이트 할 때는 평균을 내기 위해 각각의 값을 샘플의 수로 나눠서 업데이트 해야합니다.
forpass(), backprop() 메서드에 경사 하강법 적용하기
위의 행렬 계산을 적용해보겠습니다. 전체 코드는 다음과 같습니다.
class SingleLayer:
def __init__(self, learning_rate=0.1, l1=0, l2=0):
self.w = None
self.b = None
self.losses = []
self.val_losses = []
self.w_history = []
self.lr = learning_rate
self.l1 = l1
self.l2 = l2
def forpass(self, x):
z = np.dot(x, self.w) + self.b
return z
def backprop(self, x, err):
m = len(x)
w_grad = -np.dot(x.T, err) / m
b_grad = -np.sum(err) / m
return w_grad, b_grad
def activation(self, z):
a = 1 / (1 + np.exp(-z))
return a
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1)
y_val = y_val.reshape(-1, 1)
m = len(x)
self.w = np.ones((x.shape[1], 1))
self.b = 0
self.w_history.append(self.w.copy())
for _ in range(epochs):
z = self.forpass(x)
a = self.activation(z)
err = y - a
w_grad, b_grad = self.backprop(x, err)
w_grad += (self.l1*np.sign(self.w) + self.l2*self.w) / m
self.w -= self.lr*w_grad
self.b -= self.lr*b_grad
self.w_history.append(self.w.copy())
a = np.clip(a, 1e-10, 1-1e-10)
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
self.update_val_loss(x_val, y_val)
def predict(self, x):
z = self.forpass(x)
return z > 0
def score(self, x, y):
return np.mean(self.predict(x) == y.reshape(-1, 1))
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val)
a = self.activation(z)
a = np.clip(a, 1e-10, 1-1e-10)
val_loss = np.sum(-(y_val*np.log(a) + (1 - y_val)*np.log(1-a)))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val))
def reg_loss(self):
return self.l1*np.sum(np.abs(self.w)) + self.l2 / 2*np.sum(self.w**2)
forpass(), backprop()메서드에 행렬 연산 적용하기
def forpass(self, x):
z = np.dot(x, self.w) + self.b
return z
def backprop(self, x, err):
m = len(x)
w_grad = -np.dot(x.T, err) / m
b_grad = -np.sum(err) / m
return w_grad, b_grad
fit() 메서드 수정하기
이전에는 에포크를 위한 for문과 훈련 세트의 샘플을 선택하기 위한 for문이 있었는데, 이번에 사용하는 행렬연산은 훈련 세트를 전부 계산하는 배치 경사하강법을 사용하므로 훈련 세트에 적용되는 for문이 필요 없습니다.
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1)
y_val = y_val.reshape(-1, 1)
m = len(x)
self.w = np.ones((x.shape[1], 1))
self.b = 0
self.w_history.append(self.w.copy())
for _ in range(epochs):
z = self.forpass(x)
a = self.activation(z)
err = y - a
w_grad, b_grad = self.backprop(x, err)
w_grad += (self.l1*np.sign(self.w) + self.l2*self.w) / m
self.w -= self.lr*w_grad
self.b -= self.lr*b_grad
self.w_history.append(self.w.copy())
a = np.clip(a, 1e-10, 1-1e-10)
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
self.update_val_loss(x_val, y_val)
reshape(-1, 1)은 데이터 형태를 열벡터로 만들어줍니다. -1은 전체 데이터를 의미하는 것입니다. 따라서, 전체 데이터 수 x 1 크기의 열벡터로 형태를 바꿔주는 것입니다.
np.ones()함수는 주어진 행렬 크기만큼 1로 초기화합니다. x.shape[1]은 특성의 개수이므로, 크기는 특성의 개수 x 1 이고 원소의 값은 모두 1인 열벡터로 초기화합니다.
나머지 메서드 수정하기
def predict(self, x):
z = self.forpass(x)
return z > 0
def score(self, x, y):
return np.mean(self.predict(x) == y.reshape(-1, 1))
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val)
a = self.activation(z)
a = np.clip(a, 1e-10, 1-1e-10)
val_loss = np.sum(-(y_val*np.log(a) + (1 - y_val)*np.log(1-a)))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val))
데이터 전처리하기
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(x_train)
x_train_scaled = scaler.transform(x_train)
x_val_scaled = scaler.transform(x_val)
scaler.fit()은 매개변수로 들어온 데이터의 평균과 표준편차를 계산합니다. 그 후, 이 객체를 사용하여 데이터들을 전처리 해줍니다.
훈련하기
single_layer = SingleLayer(l2=0.01)
single_layer.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=10000)
single_layer.score(x_val_scaled, y_val)
에포크의 수를 1만번으로 크게 늘려줬습니다. 여기서 배치 경사 하강법이 경사 하강법보다 느린 이유가 나옵니다.
샘플이 364개일때 에포크를 100번 수행하면 경사 하강법은 (샘플의 수 X 에포크 수) 만큼의 가중치 업데이트가 일어나므로, 가중치가 36400번 업데이트 됩니다. 따라서 경사 하강법은 그래프로 그리면 흔들리지만 목표치로 빠르게 다가가는 그래프의 형태가 나옵니다.
배치 경사 하강법은 에포크의 수 만큼만 가중치 업데이트가 일어납니다. 따라서 가중치 업데이트 수를 맞춰주기 위해 에포크 수를 크게 늘려줘야합니다. 따라서 한 번의 가중치 업데이트마다 모든 샘플을 계산해야 하므로 시간이 오래 걸리지만 흔들리지 않고 목표치로 안정적으로 다가가는 그래프의 형태가 나옵니다.
성능 측정하고 그래프로 비교하기
이전 포스트와 결과는 동일하지만, 손실 함수 값이 어떻게 변하는지 확인해보겠습니다.
%matplotlib inline
plt.ylim(0, 0.3)
plt.plot(single_layer.losses)
plt.plot(single_layer.val_losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.show()
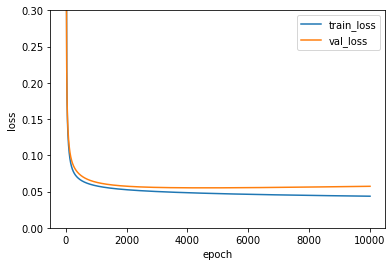
왼쪽은 경사 하강법의 손실 함수 값이고, 오른쪽은 배치 경사 하강법의 손실 함수 값입니다.
w2 = []
w3 = []
for w in single_layer.w_history:
w2.append(w[2])
w3.append(w[3])
plt.plot(w2, w3)
plt.plot(w2[-1], w3[-1], 'ro')
plt.xlabel('w[2]')
plt.ylabel('w[3]')
plt.show()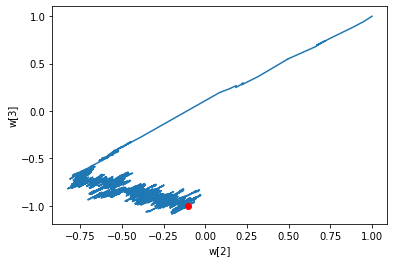

왼쪽은 경사 하강법의 가중치 변화이고, 오른쪽은 배치 경사 하강법의 가중치 변화입니다.
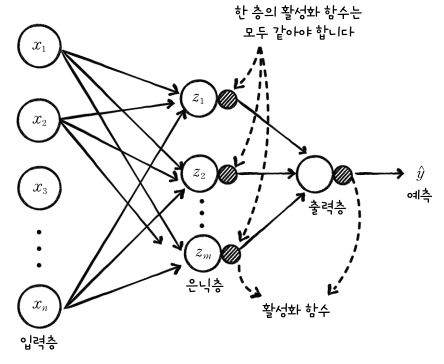
2개의 층을 가진 신경망 구현해보기
우리가 최종적으로 구현하고자 하는 신경망은 다음과 같은 형태입니다.
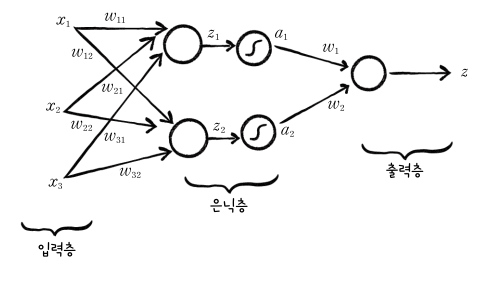
먼저 입력층과, 뉴런이 있는 은닉층을 확인해보겠습니다.

위 그림은 입력이 3개의 특성을 갖고, 2개의 뉴런이 있는 경우입니다. 위 층의 출력은 다음과 같이 나타냅니다.
$\begin{bmatrix}x_1 & x_2 & x_3 \end{bmatrix}
\begin{bmatrix}w_{11} & w_{12}\\
w_{21} & w_{22}\\
w_{31} & w_{32}
\end{bmatrix}
+\begin{bmatrix}b_1 & b_2\end{bmatrix}
= \begin{bmatrix}z_1 & z_2 \end{bmatrix}$
즉, 가중치의 인덱싱은 다음과 같습니다.

위 식을 행렬 곱으로 바꾸면 다음과 같습니다.
$\pmb{XY}_1 + \pmb{b}_1 = \pmb{Z}_1$
위의 행렬식에서 밑 첨자 1은 첫 번째 층의 가중치, 첫 번째 층의 절편, 첫 번째 층의 선형 출력이라는 의미입니다.
나중에 샘플 수와 가중치, 뉴런의 수가 많아지면 신경망의 그림과 행렬의 형태가 시각적으로 달라서 헷갈리게 되는데, 이에 대한 내용을 정리해보겠습니다.
| 입력 층에서 정해지는 것은 두가지 입니다. 샘플 수와 행렬 수 입니다. 이는 데이터에 의해 정해집니다. - 입력 층에서 특성 수가 많아지면 입력 행렬은 가로 방향으로 커지고, 가중치 행렬은 세로 방향으로 커집니다 절편에는 영향이 없습니다. - 입력 층에서 샘플 수가 많아지면 입력 행렬은 세로 방향으로 커지고, 가중치 행렬과 절편에는 영향이 없습니다. 뉴런의 개수는 우리가 마음대로 정할 수 있습니다. - 뉴런의 개수가 많아지면 가중치 행렬은 가로 방향으로 커지고, 절편 벡터는 가로 방향으로 커집니다. 입력 층과는 관계가 없습니다. - 가중치 행렬에서 세로 방향 크기는 입력 층의 특성의 개수에 의해서 결정됩니다. |
출력을 하나로 모읍니다
우리는 위스콘신 유방암 데이터 세트를 사용하여 샘플이 양성인지 음성인지를 판별하려고 합니다. 즉, 출력값이 어떤 기준값을 넘느냐 넘지 못하느냐를 갖고 판별하는데, 위의 그림을 보면 출력이 2개입니다. 따라서, 이 출력을 하나로 합쳐야 합니다.
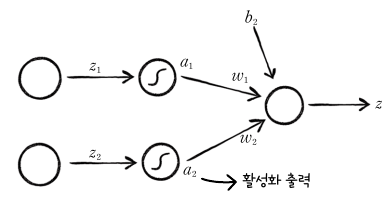
$z_1, z_2$는 마지막 뉴런으로 모으기 이전의 선형 출력값이고, $a_1, a_2$는 활성화 함수에 통과시킨 값입니다. 이제 이 값을 활성화 출력이라고 하겠습니다. 2개의 활성화 출력이 마지막 뉴런에 입력되고, 여기에 절편이 더해져 출력 $z$가 만들어집니다. 이 과정을 행렬 곱으로 나타내면 다음과 같습니다.
$\begin{bmatrix}a_1 & a_2 \end{bmatrix}
\begin{bmatrix}w_1 \\ w_2 \end{bmatrix}
+ b_2 = z$
여기서 $\pmb{A}_1$의 크기는 (전체 샘플 수, 뉴런의 수)이므로 $(m, 2)$이고, $\pmb{W}_2$의 크기는 (입력의 크기, 출력의 크기)이므로 $(2, 1)$ 입니다.
$\pmb{A}_1\pmb{W}_2 + \pmb{b}_2 = \pmb{Z}_2$
다층 신경망
다층 신경망을 그림으로 나타내면 다음과 같습니다. 활성화 함수는 뉴런 오른쪽에 작은 원으로 붙여서 나타냅니다. 이렇게 모든 뉴런이 연결되어있으면 완전 연결(fully connected) 신경망이라고 합니다.
다층 신경망에서의 경사 하강법
우리가 앞에서 봤던 다층 신경망의 구조는 다음과 같습니다.

최종적으로 $\pmb{A}_2$의 값을 보고 0.5보다 크면 양성, 그렇지 않으면 음성으로 예측합니다. 사용하는 손실 함수 $\pmb{L}$은 로지스틱 손실 함수입니다.
원하는 값으로 미분을 하는 방법은 다음과 같습니다. 아래 그림은 $\pmb{W}_2$에 대해 미분하는 그림입니다.

화살표를 따라가며, 해당 경로에 있는 값들로 미분하고, 곱해줍니다. 지금 화살표 경로상에는 $\pmb{Z}_2$가 있습니다. 따라서 손실 함수를 $\pmb{Z}_2$에 대해 미분한 후, 그 결과를 $\pmb{Z}_2$를 $\pmb{W}_2$로 미분한 값과 곱합니다.
$\frac{\partial \pmb{L}}{\partial \pmb{W}_2} = \frac{\partial \pmb{L}}{\partial\pmb{Z}_2}\frac{\partial \pmb{Z}_2}{\partial\pmb{W}_2}$
가중치에 대해 손실 함수 미분하기(출력층)
$\pmb{L}$을 $\pmb{W}_2, \pmb{Z}_2$에 대해 미분하면 다음과 같습니다.
$-(\pmb{Y} - \pmb{A}_2)\pmb{A}_1$
위 식은 이전에 보았던 로지스틱 손실 함수의 미분을 행렬로 확장한 것입니다. 즉, 아래 식을 행렬로 표현하면 됩니다.
$\frac{\partial L}{\partial w_i} = \frac{\partial L}{\partial z}\frac{\partial z}{\partial w_i} = -(y-a)x_i$
위 식에서 $-(y-a)$는 $\pmb{Y}-\pmb{A}_2)$에 해당합니다. 크기는 (샘플의 수, 1), 즉 $(m, 1)$입니다.
$x_i$는 입력값입니다. 지금 출력층에서의 입력은 바로 이전 층의 출력이므로 $\pmb{A}_1$에 해당합니다. 크기는 (샘플의 수, 뉴런의 수)입니다. 지금 우리가 구현할 신경망에서의 뉴런의 수는 2개 이므로, 크기는 $(m, 2)$입니다.
도함수 곱하기
위에서 나온 결과인 $-(\pmb{Y} - \pmb{A}_2)$와 $\pmb{A}_1$은 행렬의 크기가 다르기 때문에 바로 곱할 수 없습니다.
우리가 구하려고 했던 것은 손실 함수를 $\pmb{W}_2$에 대해 미분한 결과이므로, $\pmb{W}_2$와 같은 크기가 나와야 합니다. $\pmb{W}_2$의 크기는 (이전 층의 출력의 수(현재 층의 입력의 수), 출력 층 뉴런의 수) 이므로, $(2, 1)$입니다. 따라서, 이 형태가 나오기 위해서는 $\pmb{A}_1$를 전치(transpose)해서 $-(\pmb{Y} - \pmb{A}_2)$ 앞에다 곱해줘야 합니다. 행렬식으로 나타내면 다음과 같습니다.
$\frac{\partial \pmb{L}}{\partial \pmb{W}_2} = \frac{\partial \pmb{L}}{\partial \pmb{Z}_2} \frac{\partial \pmb{Z}_2}{\partial \pmb{W}_2} = \pmb{A}_1^T(-\pmb{Y}-\pmb{A}_2))$
위 결과의 원소 값은 모든 샘플에 대한 그래이디언트의 합이므로, 샘플 수로 나눠 평균 그래이디언트를 구해서 업데이트 해야합니다.
절편에 대해 손실함수 미분하기(출력층)
이전에 로지스틱 함수를 미분하면, 오차에 1을 곱했던 것을 기억해보세요. 가중치로 미분했던 것과 같은 방식으로 미분하면, 결과는 다음과 같습니다.
$\frac{\partial \pmb{L}}{\partial \pmb{b}_2} = \frac{\partial \pmb{L}}{\partial \pmb{Z}_2} \frac{\partial \pmb{Z}_2}{\partial \pmb{b}_2} = \pmb{1}^T(-\pmb{Y}-\pmb{A}_2))$
$\pmb{1}$은 모든 원소의 값이 1인 벡터입니다. 이 값 역시 모든 샘플의 그래이디언트의 합이므로 업데이트를 할 때에는 평균 그래이디언트로 업데이트 해야 합니다.
가중치에 대해 손실함수 미분하기(은닉층)
이번엔 가중치 $\pmb{W}_1$에 대해 미분해보겠습니다.

경로 상에는 $\pmb{Z}_2, \pmb{A}_1, \pmb{Z}_1$이 있네요. 순서대로 미분하고, 곱하면 됩니다.
$\frac{\partial \pmb{L}}{\partial \pmb{W}_1} =
\frac{\partial \pmb{L}}{\partial \pmb{Z}_2}
\frac{\partial \pmb{Z}_2}{\partial \pmb{A}_1}
\frac{\partial \pmb{A}_1}{\partial \pmb{Z}_1}
\frac{\partial \pmb{Z}_1}{\partial \pmb{W}_1}$
이제 그래이디언트가 역전파되는 모습이 잘 보이는 것 같네요.
이번에는 $\frac{\partial\pmb{Z}_1}{\partial\pmb{W}_1}$먼저 보겠습니다. $\pmb{Z}_1 = \pmb{XW}_1 + \pmb{b}_1$이므로, $\frac{\partial \pmb{Z}_1}{\partial\pmb{W}_1} = \pmb{X}$ 입니다.
다음으로는 $\frac{\partial \pmb{A}_1}{\partial\pmb{Z}_1}$를 보겠습니다. 이전에 시그모이드 함수의 도함수가 $a(1-a)$임을 배웠으므로, $\frac{\partial \pmb{A}_1}{\partial\pmb{Z}_1}$는 $\pmb{A}_1\odot(1-\pmb{A}_1)$입니다. $\odot$은 원소별 곱센을 의미합니다. $\pmb{A}_1\odot(1-\pmb{A}_1)$의 크기는 $(m, 2)$입니다.
다음으로, $\frac{\partial\pmb{Z}_2}{\partial\pmb{A}_1}$를 보겠습니다. $\pmb{Z}_2 = \pmb{A}_1\pmb{W}_2+\pmb{b}_2$이므로, $\frac{\partial\pmb{Z}_2}{\partial\pmb{A}_1} = \pmb{W}_2$입니다. $\pmb{W}_2$의 크기는 위에서 말했듯이, $(2, 1)$입니다.
마지막으로, $\frac{\partial\pmb{L}}{\partial\pmb{Z}_2}$는 출력층을 구할때의 경우와 같으므로, $\frac{\partial\pmb{L}}{\partial\pmb{Z}_2} = -(\pmb{Y-A}_2)$입니다.
도함수 곱하기
먼저, $\frac{\partial \pmb{L}}{\partial\pmb{Z}_2}$와 $\frac{\partial \pmb{Z}_2}{\partial\pmb{A}_1}$을 곱해보겠습니다. 각 값의 도함수는 $-(\pmb{Y-A}_2)$와 $\pmb{W}_2$입니다. $\pmb{Y-A}_2$의 크기는 $(m, 1)$이고 $\pmb{W}_2$의 크기는 $(2, 1)$이므로 $\pmb{W}_2$를 전치하여 곱해야 합니다. 그 결과, 행렬의 크기는 $(m, 2)$가 됩니다.
$\frac{\partial \pmb{L}}{\partial \pmb{Z}_2}\frac{\partial \pmb{Z}_2}{\partial \pmb{A}_1} = -(\pmb{Y-A}_2)\pmb{W}_2^T$
위 식의 의미는 각 샘플의 오차를 출력층의 2개의 뉴런에 반영한다는 의미입니다.
다음으로, 위 식의 결과에 $\frac{\partial \pmb{A}_1}{\partial \pmb{Z}_1}$를 곱해보겠습니다. $\frac{\partial \pmb{A}_1}{\partial \pmb{Z}_1} = \pmb{A}_1\odot(1-\pmb{A}_1)$이고, 이 값은 $-(\pmb{Y}-\pmb{A}_2)\pmb{W}_2^T$의 크기와 같으므로, 원소별 곱셈을 할 수 있습니다. 따라서 결과의 크기는 여전히 $\pmb(m, 2)$입니다.
$\frac{\partial\pmb{L}}{\partial\pmb{Z}_2}\frac{\partial\pmb{Z}_2}{\partial\pmb{A}_1}\frac{\partial\pmb{A}_1}{\partial\pmb{Z}_1}-(\pmb{Y}-\pmb{A}_2)\pmb{W}_2^T\odot\pmb{A}_1\odot(1-\pmb{A}_1)$
마지막으로, 위 값의 결과에 $\frac{\partial \pmb{Z}_1}{\partial \pmb{W}_1} = \pmb{X}$를 곱해야 합니다. $\pmb{X}$의 크기는 $(m, 3)$이고, $\frac{\partial\pmb{L}}{\partial\pmb{Z}_2}\frac{\partial\pmb{Z}_2}{\partial\pmb{A}_1}\frac{\partial\pmb{A}_1}{\partial\pmb{Z}_1}$의 크기는 $(m, 2)$이므로 $\pmb{X}$를 전치하여 곱하면 $(3, 2)$크기의 그래이디언트 행렬을 얻을 수 있습니다.
$\frac{\partial\pmb{L}}{\partial\pmb{Z}_2}\frac{\partial\pmb{Z}_2}{\partial\pmb{A}_1}\frac{\partial\pmb{A}_1}{\partial\pmb{Z}_1}\frac{\partial \pmb{Z}_1}{\partial \pmb{W}_1} = \pmb{X}^T(-(\pmb{Y}-\pmb{A}_2)\pmb{W}_2^T\odot\pmb{A}_1\odot(1-\pmb{A}_1))$
최종적으로 구한 그래이디언트 행렬인 $\pmb{W}_1$은 전체 샘플에 대한 그래이디언트의 합이므로, 각 요소 값을 전체 샘플의 수로 나눠 평균을 구하고, 이 값으로 가중치를 업데이트 합니다.
절편에 대해 손실함수 미분하고, 도함수 곱하기(은닉층)
가중치에 대한 미분 과정과 같으므로 과정은 생략합니다. 최종 결과의 크기는 $(1, 2)$입니다.
$\frac{\partial \pmb{L}}{\partial\pmb{b}_1} = \frac{\partial\pmb{L}}{\partial\pmb{Z}_2}\frac{\partial\pmb{Z}_2}{\partial\pmb{A}_1}\frac{\partial\pmb{A}_1}{\partial\pmb{Z}_1}\frac{\partial \pmb{Z}_1}{\partial \pmb{b}_1} = \pmb{1}^T(-(\pmb{Y}-\pmb{A}_2)\pmb{W}_2^T\odot\pmb{A}_1\odot(1-\pmb{A}_1))$
2개의 층을 가진 신경망 구현하기
이전에 사용했던 SingleLayer 클래스를 상속하여 새로운 클래스를 만듭니다.
전체 코드입니다.
class DualLayer(SingleLayer):
def __init__(self, units=10, learning_rate=0.1, l1=0, l2=0):
self.units = units
self.w1 = None
self.b1 = None
self.w2 = None
self.b2 = None
self.a1 = None
self.losses = []
self.val_losses = []
self.lr = learning_rate
self.l1 = l1
self.l2 = l2
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1
self.a1 = self.activation(z1)
z2 = np.dot(self.a1, self.w2) + self.b2
return z2
def backprop(self, x, err):
m = len(x)
w2_grad = np.dot(self.a1.T, -err) / m
b2_grad = np.sum(-err) / m
err_to_hidden = np.dot(-err, self.w2.T)*self.a1*(1 - self.a1)
w1_grad = np.dot(x.T, err_to_hidden) / m
b1_grad = np.sum(err_to_hidden, axis=0) / m
return w1_grad, b1_grad, w2_grad, b2_grad
def init_weights(self, n_features):
self.w1 = np.ones((n_features, self.units))
self.b1 = np.zeros(self.units)
self.w2 = np.ones((self.units, 1))
self.b2 = 0
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1)
y_val = y_val.reshape(-1, 1)
m = len(x)
self.init_weights(x.shape[1])
for _ in range(epochs):
a = self.training(x, y, m)
a = np.clip(a, 1e-10, 1-1e-10)
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
self.update_val_loss(x_val, y_val)
def training(self, x, y, m):
z = self.forpass(x)
a = self.activation(z)
err = y - a
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
w1_grad += (self.l1*np.sign(self.w1) + self.l2*self.w1) / m
w2_grad += (self.l1*np.sign(self.w2) + self.l2*self.w2) / m
self.w1 -= self.lr*w1_grad
self.b1 -= self.lr*b1_grad
self.w2 -= self.lr*w2_grad
self.b2 -= self.lr*b2_grad
return a
def reg_loss(self):
return self.l1*(np.sum(np.abs(self.w1)) + np.sum(np.abs(self.w2))) +\
self.l2 / 2*(np.sum(self.w1**2) + np.sum(self.w2**2))
1. SingleLayer 상속하기
class DualLayer(SingleLayer):
def __init__(self, units=10, learning_rate=0.1, l1=0, l2=0):
self.units = units
self.w1 = None
self.b1 = None
self.w2 = None
self.b2 = None
self.a1 = None
self.losses = []
self.val_losses = []
self.lr = learning_rate
self.l1 = l1
self.l2 = l2은닉층의 뉴런의 개수를 지정하는 변수가 추가되었습니다. 기존에 설명할 때는 뉴런이 2개인 경우였습니다.
이제 이렇게 층이 깊어지면 가중치의 개수가 너무 많아지므로, 가중치의 변화를 확인하기가 어렵습니다. 따라서 이제부터 가중치의 변화는 기록하지 않겠습니다.
2. forpass() 메서드 수정하기
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1
self.a1 = self.activation(z1)
z2 = np.dot(self.a1, self.w2) + self.b2
return z2은닉층과 출력층의 정방향 계산을 수행합니다.
3. backprop() 메서드 수정하기
def backprop(self, x, err):
m = len(x)
w2_grad = np.dot(self.a1.T, -err) / m
b2_grad = np.sum(-err) / m
err_to_hidden = np.dot(-err, self.w2.T)*self.a1*(1 - self.a1)
w1_grad = np.dot(x.T, err_to_hidden) / m
b1_grad = np.sum(err_to_hidden, axis=0) / m
return w1_grad, b1_grad, w2_grad, b2_grad
error_to_hidden은 미분 결과에서 아래 그림에 표시된 부분을 의미합니다.

4. fit() 메서드 수정하기
def init_weights(self, n_features):
self.w1 = np.ones((n_features, self.units))
self.b1 = np.zeros(self.units)
self.w2 = np.ones((self.units, 1))
self.b2 = 0
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1)
y_val = y_val.reshape(-1, 1)
m = len(x)
self.init_weights(x.shape[1])
for _ in range(epochs):
a = self.training(x, y, m)
a = np.clip(a, 1e-10, 1-1e-10)
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
self.update_val_loss(x_val, y_val)
def training(self, x, y, m):
z = self.forpass(x)
a = self.activation(z)
err = y - a
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
w1_grad += (self.l1*np.sign(self.w1) + self.l2*self.w1) / m
w2_grad += (self.l1*np.sign(self.w2) + self.l2*self.w2) / m
self.w1 -= self.lr*w1_grad
self.b1 -= self.lr*b1_grad
self.w2 -= self.lr*w2_grad
self.b2 -= self.lr*b2_grad
return afit() 메서드를 세 부분으로 나눕니다.
7. reg_loss() 메서드 수정하기
def reg_loss(self):
return self.l1*(np.sum(np.abs(self.w1)) + np.sum(np.abs(self.w2))) +\
self.l2 / 2*(np.sum(self.w1**2) + np.sum(self.w2**2))은닉층과 출력층의 가중치에 대한 L1, L2 손실을 계산합니다.
모델을 훈련하고 평가하기
dual_layer = DualLayer(l2=0.01)
dual_layer.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=20000)
dual_layer.score(x_val_scaled, y_val)
손실 그래프 분석하기
plt.ylim(0, 0.3)
plt.plot(dual_layer.losses)
plt.plot(dual_layer.val_losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.show()
손실 그래프가 SingLayer보다 천천히 감소합니다. 이는 가중치의 수가 훨씬 많아서 학습하는데 시간이 오래 걸리기 때문입니다. 우리가 사용한 데이터의 특성은 30개입니다. 따라서 SingLayer에서는 학습할 가중치가 30개뿐이지만, DualLayer에서는 은닉층의 뉴런을 10개로 하였으므로, 은닉층에서 가중치만 300개, 절편이 10개여서 310개의 파라미터를 학습해야 합니다. 출력층에서는 10개의 뉴런의 출력을 모아주는 뉴런이 1개 있으므로, 각 뉴런에서 나오는 가중치들 10개와 절편 1개가 필요하므로, 학습해야할 파라미터는 총 321개 입니다.
가중치 랜덤하게 초기화하기
손실 그래프를 보니 곡선이 매끄럽지 않는데, 이는 손실 함수가 감소하는 방향을 제대로 찾지 못했기 때문으로 보입니다. 지금까지는 가중치를 1로 초기화했으나, 이번에는 정규 분포를 따르는 무작위의 값으로 초기화해보겠습니다. 참고로, 가중치를 초기화하는 방법은 이 외에도 여러가지가 있습니다.
가중치 초기화를 위한 init_weight() 메서드 수정하기
class RandomInitNetwork(DualLayer):
def init_weights(self, n_features):
np.random.seed(42)
self.w1 = np.random.normal(0, 1, (n_features, self.units))
self.b1 = np.zeros(self.units)
self.w2 = np.random.normal(0, 1, (self.units, 1))
self.b2 = 0
np.random.normal() 함수를 사용하여 랜덤하게 초기화합니다. 매개변수는 순서대로 평균, 표준편차, 배열 크기 입니다.
이제 손실 함수를 확인해보겠습니다.
random_init_net = RandomInitNetwork(l2=0.01)
random_init_net.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=500)
plt.ylim(0, 0.7)
plt.plot(random_init_net.losses)
plt.plot(random_init_net.val_losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.show()
미니 배치를 사용하여 모델을 훈련하기
미니 배치 경사 하강법은 에포크마다 일부의 데이터만 사용하여 정방향 계산을 수행하고, 그래이디언트를 구하여 가중치를 업데이트합니다. 예를 들어, 학생에게 1000개의 시험 예상 문제를 줍니다. 학생들이 이 문제를 푸는것은 신경망에서 학습하는 것과 같고, 틀린 문제를 확인하여 오답풀이를 하는 것은 가중치를 업데이트 하는것과 같습니다.
이 때, 문제를 하나 풀때마다 답을 확인하여 오답풀이를 하는 것은 경사 하강법과 같습니다. 문제를 일부 풀고 오답풀이를 하는 것은 미니 배치 경사 하강법입니다. 문제를 모두 다 풀고 오답풀이를 하는 것은 배치 경사 하강법입니다.
미니 배치 경사 하강법은 작게 나눈 미니 배치만큼의 데이터를 사용하여 가중치를 업데이트 합니다. 미니 배치의 크기는 보통 16, 32, 64 등 2의 배수를 사용하는데, 이는 GPU를 효율적으로 사용하기 위함입니다.
여기서 미니 배치의 크기가 1이면 경사 하강법이고, 샘플의 수와 같으면 배치 경사 하강법입니다. 중요한 점은 미니 배치의 최적값은 정해진 값이 아니며, 이 또한 우리가 튜닝해야 하는 하이퍼파라미터입니다.
미니 배치 경사 하강법 구현하기
앞에서 구현한 RandomInitNetwork 클래스를 상속하여 새로운 클래스를 만듭니다.
다음은 전체 코드입니다.
class MinibatchNetwork(RandomInitNetwork):
def __init__(self, units=10, batch_size=32, learning_rate=0.1, l1=0, l2=0):
super().__init__(units, learning_rate, l1, l2)
self.batch_size = batch_size
def gen_batch(self, x, y):
length = len(x)
bins = length // self.batch_size
if length % self.batch_size:
bins += 1
indexes = np.random.permutation(np.arange(len(x)))
x = x[indexes]
y = y[indexes]
for i in range(bins):
start = self.batch_size*i
end = self.batch_size*(i+1)
yield x[start:end], y[start:end]
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y_val = y_val.reshape(-1, 1)
self.init_weights(x.shape[1])
np.random.seed(42)
for i in range(epochs):
loss = 0
for x_batch, y_batch in self.gen_batch(x, y):
y_batch = y_batch.reshape(-1, 1)
m = len(x_batch)
a = self.training(x_batch, y_batch, m)
a = np.clip(a, 1e-10, 1-1e-10)
loss += np.sum(-(y_batch*np.log(a) + (1-y_batch)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / len(x))
self.update_val_loss(x_val, y_val)
1. MinibatchNetwork 클래스 구현하기
class MinibatchNetwork(RandomInitNetwork):
def __init__(self, units=10, batch_size=32, learning_rate=0.1, l1=0, l2=0):
super().__init__(units, learning_rate, l1, l2)
self.batch_size = batch_sizesuper()에 대한 내용은 링크를 참조하세요.
2. gen_batch() 메서드 만들기
입력으로 주어진 행렬을 나눠 여러 개의 배치를 만듭니다.
def gen_batch(self, x, y):
length = len(x)
bins = length // self.batch_size
if length % self.batch_size:
bins += 1
indexes = np.random.permutation(np.arange(len(x)))
x = x[indexes]
y = y[indexes]
for i in range(bins):
start = self.batch_size*i
end = self.batch_size*(i+1)
yield x[start:end], y[start:end]yield에 대한 내용은 링크를 참조하세요.
3. fit() 메서드 수정하기
경사 하강법에서 에포크마다 수행했던 for문을 행렬을 사용한 배치 경사하강법을 구현하며 지웠었는데, 이제 다시 에포크마다 일부 샘플들을 사용하는 반복문이 필요하므로, 그 부분을 다시 구현합니다.
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y_val = y_val.reshape(-1, 1)
self.init_weights(x.shape[1])
np.random.seed(42)
for i in range(epochs):
loss = 0
for x_batch, y_batch in self.gen_batch(x, y):
y_batch = y_batch.reshape(-1, 1)
m = len(x_batch)
a = self.training(x_batch, y_batch, m)
a = np.clip(a, 1e-10, 1-1e-10)
loss += np.sum(-(y_batch*np.log(a) + (1-y_batch)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / len(x))
self.update_val_loss(x_val, y_val)
4. 훈련하기
minibatch_net = MinibatchNetwork(l2=0.01, batch_size=32)
minibatch_net.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=500)
print(minibatch_net.score(x_val_scaled, y_val))
plt.ylim(0, 0.7)
plt.plot(minibatch_net.losses)
plt.plot(minibatch_net.val_losses)
plt.ylabel('loss')
plt.xlabel('iteration')
plt.legend(['train_loss', 'val_loss'])
plt.show()
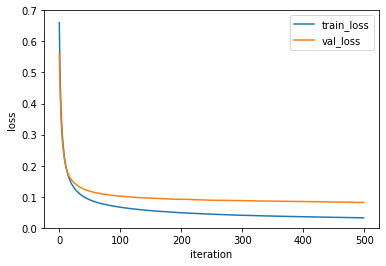

왼쪽의 그래프가 미니 배치 경사 하강법이고, 오른쪽의 그래프가 배치 경사 하강법입니다. 수렴 속도가 빨라진 것을 확인할 수 있습니다.
이번엔 배치의 크기를 늘려보겠습니다.
minibatch_net = MinibatchNetwork(l2=0.01, batch_size=128)
minibatch_net.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=500)
print(minibatch_net.score(x_val_scaled, y_val))
plt.ylim(0, 0.7)
plt.plot(minibatch_net.losses)
plt.plot(minibatch_net.val_losses)
plt.ylabel('loss')
plt.xlabel('iteration')
plt.legend(['train_loss', 'val_loss'])
plt.show()
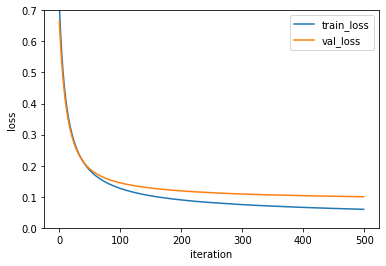
손실 그래프가 좀 더 안정적으로 바뀌었지만, 수렴하는데는 더 오래 걸리는 것을 확인할 수 있습니다. 일반적으로 미니 배치의 크기는 32~512의 값을 지정합니다.
사이킷런을 사용해 다층 신경망 훈련하기
사이킷런에는 이미 신경망 알고리즘이 구현되어있습니다. 분류를 위한 클래스는 MLPClassifier, 회귀를 위한 클래스는 MLPRegressor 입니다.
from sklearn.neural_network import MLPClassifier
mlp = MLPClassifier(hidden_layer_sizes=(10, ), activation='logistic',
solver='sgd', alpha=0.01, batch_size=32,
learning_rate_init=0.1, max_iter=500)
mlp.fit(x_train_scaled, y_train)
mlp.score(x_val_scaled, y_val)hidden_layer_sizes : 은닉층의 크기를 정의합니다. 10개의 뉴런을 가진 1개의 층을 만드려면 위와 같이 설정하고, 2개의 층을 만드려면 (10, 10)과 같이 설정합니다.
activation : 활성화 함수를 설정합니다.
solver : 경사 하강법의 종류를 설정합니다.
alpha : L2 규제의 크기를 설정합니다.
나머지 파라미터는 이름만 봐도 알 수 있을 것입니다.
사이킷런을 사용한 훈련 결과는 우리가 구현한 결과와 약간 다른데, 이는 기술적으로 약간 차이가 있기 때문입니다.