6. Robot Perception
이 글은 Sebastian thrun의 Probabilistic Robotics를 보고 내용을 정리한 글이며, 나름 쉽게 표현하기 위해서 의역을 한 부분이 있습니다.
6.1. Introduction
확률적 로보틱스는 센서 측정에서의 노이즈를 분명하게 모델링합니다. 그러한 모델은 로봇의 센서에 내재하는 불확실성을 설명합니다. 이 측정 모델은 조건부 확률 분포 $p(z_t | x_t, m)$으로 모델링 되며, 여기서 $x_t$는 로봇의 pose, $z_t$는 시간 $t$에서의 측정값, $m$은 환경의 지도(map of environment) 입니다
모바일 로봇이 센서를 사용하여 주변 환경을 인식하는 기본적인 문제를 묘사하기 위해, 그림 6.1 (a)는 초음파 거리 스캔(sonar range scan) 24개를 원형으로 배열하여 복도에서의 데이터를 얻는 일반적인 상황을 보여줍니다.
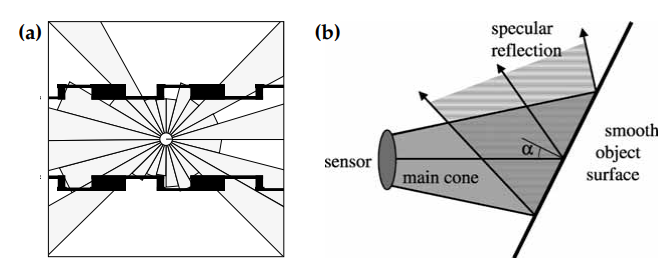
여기서 각각 센서의 측정은 회색 영역으로 나타냈고, 그 환경은 검은색으로 나타냈습니다. 대부분의 이 측정들은 원뿔 모양의 측정에서 가장 가까운 object의 거리에 대응되는데, 가끔 몇몇 데이터는 object를 탐지하는데 실패하기도 합니다.
초음파가 주변의 object를 정확하게 측정할 수 없는 것은 보통 센서의 노이즈 라고 표현됩니다. 엄밀히 말해서, 이 노이즈는 예측이 가능한데, 매끈한 평면을 측정할 때 보통 거울같은 반사가 일어나며, 그 벽(매끈한 평면)은 그 음파의 거울이 됩니다. 이 것은 그 음파가 어떤 각도로 표면에 입사할 때, 이를 확률적으로 나타낼 수 있습니다. 그림 6.1의 (b)는 반사된 음파가 초음파 센서가 아닌 다른 방향을 향할 수 있다는 것을 보여줍니다. 이로 인해서 측정 범위 내에서의 가장 가까운 장애물까지의 실제 거리와 비교했을 때 지나치게 큰 범위로 감지하는 결과가 나오게 됩니다. 이런 상황이 발생하기 위한 likelihood는 표면의 물질, 평면의 법선과 센서의 main cone의 각도, main cone의 넓이, 센서의 민감도(sensitivity)같이 몇 가지 속성에 의존합니다.
그림 6.2는 일반적인 2D 레이저 거리 스캐너(LRF, Laser Range Finder)에 의한 레이저 거리 스캔(laser range scan)을 보여줍니다.
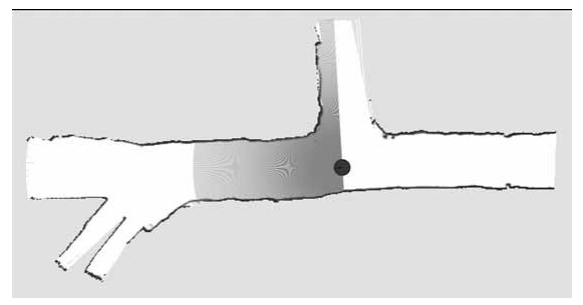
레이저 센서도 초음파 센서와 비슷하게 신호를 방출하고 돌아오는 신호를 기록하는데, 이 센서는 레이저 빔을 그 신호로 사용합니다. 초음파 센서와 가장 중요한 차이점은 레이저는 훨씬 집중된 빔(focused beam)을 사용한다는 것입니다.
일반적으로, 센서 모델이 더 정확할수록 더 좋은 결과가 나오지만, 물리적 현상의 복잡함 때문에 종종 센서를 정확하게 모델링하는것은 불가능합니다.
종종 센서의 응답특성은 확률적 로보틱스 알고리즘에서 명시하는 것을 선호하지 않는 변수에 의존합니다(벽 표면의 물질 또는 색깔같은 그런 경우를 말합니다. 사실, LRF의 경우 검은색보다 흰색 물체를 더 잘 인식합니다.) 확률적 로보틱스는 확률적으로 센서의 부정확성을 나타내는데, measurement process를 deterministic한 함수 $z_t = f(x_t)$라고 하는 대신 조건부 독립 확률 밀도 $p(z_t | x_t)$로 모델링합니다. 즉, 센서 모델의 불확실성은 그 모델을 non-deterministic한 형태로 나타내는 것으로 표현될 수 있습니다.
많은 센서들은 하나 이상의 숫자적인 측정값(numerical measurement value)을 생성합니다. 예를 들어, 카메라는 전체 값의 배열을 생성합니다(밝기, saturation, 색). 우리는 이제 다음과 같이 측정 $z_t$에서의 측정값들의 수를 $K$로 나타낼 것입니다.
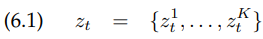
여기서 $z_t^k$는 한 개의 측정값입니다. 확률 $p(z_t | x_t, m)$은 각각 측정값 likelihood의 곱에 의해 얻게됩니다(조건부 독립을 생각하세요).
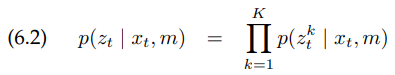
엄밀히 말해서, 이 값은 각각의 측정에서 노이즈들이 이전에 마르코프 가정이 시간에 대해 독립이라는 것 처럼 모두 독립이어야 합니다.
6.2. Maps
process of generating measurements를 표현하기 위해, 우리는 그 measurement가 만들어진 환경을 명시해야 합니다. 환경의 map이란 그 환경의 object와 그것들의 위치의 리스트입니다. 공식적으로, 맵 $m$은 어떤 환경 안에서의 object와 그 속성의 리스트입니다.
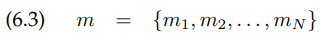
여기서 $N$은 그 환경에서의 전체 object의 수이며, 각 $m_n, \quad (1<=n<=M)$은 그 속성을 나타냅니다. 지도는 보통 feature-based 또는 location-based중 하나의 방법으로 인덱싱 됩니다.
feature-based 지도에서, $n$은 feature의 인덱스를 나타냅니다. $m_n$의 값은 feature의 속성 옆에, 그 feature의 Cartesian location을 포함합니다. location-based 지도에서, 인덱스 $n$은 특정한 위치에 대응됩니다. 평면 지도에서, 이는 일반적으로 $m_n$이라고 하는 대신 $m_{(x, y)}$으로 지도의 요소를 나타내는데, $m_{(x, y)}$가 특정한 world coordinate, $(x, y)$의 속성이라는 것을 정확하게 나타내기 위함입니다.
location-based 지도는 volumetric한데, world에서의 모든 위치의 label을 제공하기 때문입니다. 즉, volumetric한 지도는 object에 대한 정보 뿐 아니라 free-space같이 object가 없는 위치에 대한 정보를 갖고있습니다.
feature-baased 지도는 단지 특정한 위치에서의 환경의 shape만을 명시합니다. 즉, 그 지도에 포함된 object의 위치입니다.