이 글은 Sebastian thrun의 Probabilistic Robotics를 보고 내용을 정리한 글이며, 나름 쉽게 표현하기 위해서 의역을 한 부분이 있습니다.
1. The Basic Measurement Algorithm
앞으로 나올 모델은 4종류의 측정 오차를 포함합니다. 이는 작은 측정 노이즈(small measurement noise), 예상치 못한 물체로 인한 오차(errors due to unexpected objects), 물체 감지의 실패로 인한 오차(errors due to failures to detect objects), 설명할 수 없는 무작위 오차(random unexplained noise)입니다. 따라서 요구되는 확률 모델 $p(z_t | x_t, m)$은 이 4가지 확률 밀도의 합이며, 각각은 특정한 종류의 오차에 해당됩니다.
1. Correct range with local measurement noise
Ideal world에서, 거리 센서는 가장 근처에 있는 object까지의 거리를 항상 정확하게 측정합니다. object까지의 거리 $z_t^{k*}$를 측정값 $z_t^k$의 "true" range라고 하겠습니다(즉, $z_t^k$는 센서가 측정한 거리이고 $z_t^{k*}$는 실제 거리입니다.) location-based map에서는 $z_t^{k*}$는 ray casting에 의해 결정될 수 있고, feature-based map에서는 보통 measurement cone 내부의 가장 가까운 feature를 찾는 것에 의해 얻게 됩니다. 하지만, 센서가 가장 가까운 object의 거리를 맞게 측정한다고 하더라도 이 값은 오차를 조건으로(subject to error) 합니다. 이 오차는 거리 측정 센서의 해상도의 한계나 측정 신호의 대기(atmospheric)의 효과 등 이런 것을 말합니다. 이 measurement noise는 보통 평균이 $z_t^{k*}$이고 표준편차가 $\sigma _{hit}$인 좁은 폭의 가우시안 분포로 모델링 됩니다. 우리는 이 가우시안을 $p_{hit}$라고 하겠습니다. 그림 6.3 (a)는 특정 값 $z_t^{k*}$에 대한 확률 밀도 $p_{hit}$를 보여줍니다.

실제로는 거리 센서에 의해 측정된 값은 구간 $\left[0; z_{max}\right]$로 제한되며, $z_{max}$는 센서의 최대 측정 범위입니다. 따라서, 측정 확률은 다음과 같이 주어집니다.
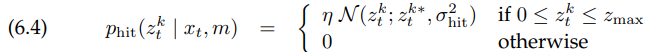
여기서 $z_t^{k*}$는 $x_t$로부터 계산되었으며 $m$은 ray casting을 통해서 계산되고, $\mathcal{N}(z_t^k;z_t^{k*},\sigma _{hit}^2)$는 평균이 $z_t^{k*}$이고 표준편차가 $\sigma _{hit}$인 univariate normal distribution을 나타냅니다. 즉,

여기서 정규화 상수(normalizer) $\eta$는
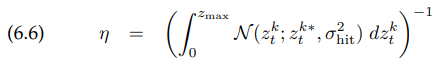
여기서 표준편차 $\sigma _{hit}$는 measurement model의 intrinsic noise parameter입니다. 나중에 이 파라미터를 어떻게 세팅하는지에 대해 설명할 것입니다.
2. Unexpected objects
모바일 로봇의 환경은 dynamic 하지만, map $m$은 static 합니다. 그 결과, map에 포함되지 않은 object는 거리 센서가 예상치 못한, 예상보다 짧은 측정 결과를 내도록 합니다. 움직이는 object의 전형적인 예시로는 로봇의 operational space에 있는 사람들입니다. 이러한 object를 다루기 위한 방법으로는 그들을 state vector의 일부로 취급하고 그 위치를 추정하는 것인데, 훨씬 더 쉬운 방법으로는 그들을 그냥 센서의 noise로 취급하는 것입니다. 이들을 센서의 noise로 취급하면, 그 object는 센서가 측정했을 때, $z_t^{k*}$보다 작거나 같은 값을 가진다는 속성이 있습니다(로봇과 지도상의 object 사이에 있을 것이니 당연히 $z_t^{k*}$보다는 작거나 같아야 합니다.)
sensing unexpected objects의 likelihood는 거리가 증가함에 따라 감소합니다. 예를 들어, 독립적으로 두 사람이 있다고 상상해보겠습니다. 이들은 가까운 센서의 perceptual field에서 고정된 값의 같은 likelihood를 갖고 있다고 하겠습니다. 한 명은 센서와의 거리가 $r_1$이고, 다른 한 명은 $r_2$이며, $r_1 < r_2$라고 가정하겠습니다. 이렇게 되면 우리는 $r_1$을 측정할 확률이 $r_2$보다 크게 됩니다. 첫 번째 사람이 존재할 때마다, 센서는 $r_1$을 측정하게 될 것입니다. $r_2$를 측정하기 위해서는 첫 번째 사람이 없어지고, 두 번째 사람이 존재해야 합니다.
이 상황은 수학적으로 지수 함수 분포에 의해 묘사됩니다. 이 분포의 파라미터는 $\lambda _{short}$이고, 이 또한 measurement model의 intrinsic parameter입니다. 이 지수 함수 분포의 정의에 따라 우리는 다음과 같은 방정식 $p_{short}(z_t^k|x_t, m)$을 얻게 됩니다.

위 지수함수는 구간이 $\left[0;z_t^{k*}\right]$이기 때문에 이전의 경우처럼 우리는 normalizer $\eta$가 필요합니다. 왜냐하면 이 구간에서의 CDF는 다음과 같기 때문입니다.

따라서 $\eta$는 다음과 같이 주어집니다.
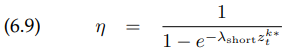
그림 6.3의 (b)는 이 확률 밀도를 그래프로 보여줍니다. 이 확률 밀도는 측정 범위 $z_t^k$이내에 포함되는 것을 보여줍니다.
3. Failures
가끔, object감지를 하지 못하는 경우가 있는데, 예를 들어, 초음파 센서의 경우 정반사로 인해 이런 현상이 자주 일어납니다. LRF(Laser Range Finder)의 경우에는 빛을 흡수하는 검은색의 경우 감지에 실패하는 경우도 있고, 밝은 햇빛 아래에서도 감지를 잘 못합니다. 일반적인 sensor failure는 max-range measurement인데, 센서가 가능한 최대의 값 $z_{max}$를 리턴하는 경우입니다. 이런 경우는 꽤 자주 일어나는데, 이는 measurement model에서 max-range measurement를 정확히 모델링하기 위해 필요합니다.
이런 경우 우리는 모델링을 위해 $z_{max}$를 중심으로 하는 point-mass distribution을 사용합니다.

여기서 $I$는 매개변수가 true인 경우는 값이 1이고 그 외의 경우는 값이 0인 indicator function입니다. 엄밀히 말해서, $p_{max}$는 불연속 분포이기 때문에 확률 밀도 함수를 갖지 않습니다. 하지만, 여기서 제안하는 센서의 측정을 evaluating 하는 수학적 모델은 확률 밀도 함수가 존재하지 않는다는 것에 의한 영향을 받지는 않습니다(그림 6.3에서 우리는 $p_{max}$를 중심이 $z_{max}$인 아주 좁은 uniform distribution으로 나타냈는데, 이 때문에 확률 밀도가 존재한다는 것처럼 가장할 수 있습니다.)
4. Random measurements
마지막으로, 거리 센서는 가끔 전혀 설명할 수 없는 측정값(entirely unexplainable measurements)을 측정하기도 합니다. 이러한 현상을 간단하게 모델링하기 위해, 우리는 센서의 측정 범위 $\left[0;z_{max}\right]$에 넓게 퍼진 uniform distribution으로 모델링합니다. 그림 6.3의 (d)는 식 (6.11)을 보여줍니다.

위에서 소개된 4개의 다른 분포들은 이제 $z_{hit}, z_{short}, z_{max}, z_{rand}$라고 정의된 가중치 파라미터들을 곱하여 합쳐지게 됩니다. 이때, $z_{hit} + z_{short} + z_{max} + z_{rand} = 1$ 입니다.

각각 확률 밀도의 선형 결합에 의한 결과의 일반적인 확률 밀도 함수는 그림 6.4에 나타내었습니다.

위 그림을 보면 알 수 있듯이, 4개의 확률 밀도 모델의 기본적인 특성이 그림 6.4에 여전히 드러나있습니다.
알고리즘 beam_range_finder_model에 적용된 거리 측정 모델은 table 6.1. 에 나타내었습니다.

이 알고리즘의 입력은 complete range scan $z_t$, 로봇의 pose $x_t$, map $m$입니다. 바깥쪽 loop(line 2와 7)에서는 각각의 센서 빔 $z_t^k$의 likelihood를 식(6.2)과 같이 곱합니다.

line 4는 특정 센서 측정의 noise-free range를 계산하기 위해 ray casting을 적용합니다. 각각의 range measurement $z_t^k$는 식(6.12)을 적용하여 line 5에서 계산됩니다. $z_t$에서의 모든 센서 측정값 $z_t^k$에 대한 반복을 통해 이 알고리즘은 우리가 요구하는 확률 $p(z_t |x_t, m)$을 리턴하게 됩니다.
2. Adjusting the Intrinsic Model Parameters
위에서 소개한 센서 모델의 파라미터들 $z_{hit}, z_{short}, z_{max}, z_{rand}$은 파라미터 $\sigma _{hit}, \lambda _{short}$도 포함합니다. 이제 이 모든 intrinsic parameter의 집합을 $\Theta$라고 하겠습니다.
이 intrinsic parameter를 결정하기 위한 방법 중 하나는 데이터에 의존합니다. 그림 6.5는 일반적인 사무실 환경에서 측정한 10,000개의 측정값들입니다.

두 그림은 모두 expected range가 약 3미터인 측정을 보여줍니다. 왼쪽의 그림은 초음파 센서, 오른쪽 그림은 레이저 센서를 이용한 데이터를 보여줍니다. 두 그림에서 $x$축은 데이터의 번호(1부터 10,000)이고, $y$축은 센서에 의해 측정된 거리입니다.
두 센서 모두 대부분의 측정값은 올바른 측정값 범위에 있지만, 두 데이터의 양상은 상당히 다른데, 초음파 센서는 노이즈와 오차가 더 심한 것을 볼 수 있습니다. 이 센서는 장애물을 감지하는데 자주 실패하며, 따라서 센서의 최대 측정값을 리턴합니다. 대조적으로, 레이저 센서는 더 정확하긴 하지만 그래도 가끔 잘못된 측정값을 나타내긴 합니다.
intrinsic parameter $\Theta$를 정확하게 조절하는 방법은 직접 구하는 것인데, 그냥 실험해보면서 그 실험에 맞는 데이터가 나올 때까지 단순히 계속 파라미터를 바꿔가면서 시도해보는 것입니다.
좀 더 원칙적인 다른 방법은, 실제 데이터로부터 이 파라미터를 가르치는 것(learn)입니다. 이 방법은 로봇의 위치 $X = {x_i}$, map $m$에서의 reference data set $Z = {z_i}$의 likelihood를 최대화하는 것인데, 여기서 $z_i$는 실제 데이터 측정값, $x_i$는 측정이 이루어진 pose, $m$은 측정이 이루어진 map입니다. 여기서 data $Z$의 likelihood는 다음과 같이 주어집니다.

우리의 목표는 likelihood를 최대화하는 $\Theta$를 찾는 것입니다. 이렇게 데이터의 likelihood를 최대화하는 estimator나 알고리즘을 maximum likelihood estimator 또는 ML estimator라고 합니다.
table 6.2. 는 learn_intrinsic_parameters 알고리즘을 보여주는데, 이 알고리즘은 intrinsic parameter에 대한 최대 likelihood를 계산하기 위한 알고리즘입니다.

위 알고리즘은 초기에 intrinsic parameters $\sigma _{hit}, \lambda _{short}$의 좋은 초기화를 필요로 합니다. line 3에서 9를 통해, 위 알고리즘은 임시 변수를 추정합니다. 각 $e_{i,\tt xxx }$는 "xxx"에 의한 측정값 $z_i$의 확률이며, 이때 "xxx"는 센서 모델의 4가지 양상 hit, short, max, random 중 하나입니다. 다음으로, line 10~15를 통해 intrinsic parameter를 추정합니다. 하지만, 이 intrinsic parameters는 이전에 계산된 기댓값들의 함수입니다. 이 intrinsic parameters를 조절하는 것은 기댓값을 변하게 만들며($\sigma _{hit}$와 $\lambda _{short}$가 바뀌면서 기댓값 계산에 영향을 줍니다), 이 때문에 알고리즘은 반복적으로 수행되어야 합니다. 하지만, 실제로 이 반복은 매우 빠르게 수렴하며, 수십 번의 반복 정도면 좋은 결과를 만들기에 충분합니다.
그림 6.6. 은 learn_intrinsic_parameters에 의해 계산된 ML measurement model의 예제입니다.
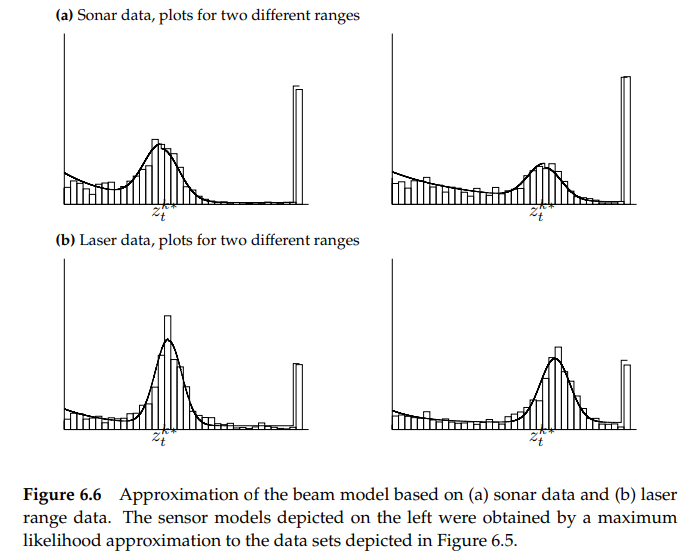
위 그래프는 그림 6.5의 데이터를 이용한 결과입니다. 첫 행은 초음파 센서를 이용한 결과이고 두 번째 행은 레이저 센서를 이용한 데이터입니다. 각 열의 결과는 "true" range를 다르게 한 결과입니다.
위 그래프에서 볼 수 있는 차이점은 거리 $z_t^{k*}$가 작을수록 측정값이 더 정확하다는 것입니다. 즉, 측정 거리가 긴 오른쪽 그래프보다 측정 거리가 짧은 왼쪽 열의 가우시안 그래프가 더 좁은 형태를 보이는 것을 알 수 있습니다. 또한, 레이저 센서가 초음파 센서보다 더 정확하다는 것도 알 수 있습니다. 우리가 주목해야 할 또 다른 중요한 점은, 상대적으로 큰 short와 random measurement의 likelihood입니다. 이 큰 error likelihood는 장단점이 있는데, 단점 중 하나는 hit와 random measurement의 likelihood의 차이가 작기 때문에 각각의 sensor reading의 정보를 줄인다는 것입니다. 장점은 오랜 시간 동안 로봇의 경로를 막는 사람들같이 unmodeled systematic perturbations에 덜 예민하다는 것입니다.
그림 6.7. 은 동작하는 learned sensor model입니다. 그림 6.7. (a)는 180도 레이저 스캔을 보여줍니다.

위 그림에서 로봇은 이전에 얻은 occupancy grid map에서 true pose에 놓여 있습니다. 그림 6.7. 의 (b)는 로봇 환경의 map을 따라 likelihood $p(z_t|x_t, m)$이 분포한 모습을 보여줍니다. 색이 더 어두울수록 로봇이 있을 확률이 더 높다는 것을 뜻합니다. 위 그림에서 보이듯이, likelihood가 높은 구역은 대부분 복도에 있습니다. 이렇게 확률 질량 함수가 복도에 넓게 퍼져있다는 것은 하나의 센서로는 로봇의 정확한 위치를 찾기 어렵다는 것을 뜻하는데, 이는 복도의 대칭성 때문입니다. 사후 확률이 두 개의 좁은 수평 bands에서 계산된 것은 로봇의 방향을 알 수 없다는 것입니다.
쉽게 설명하자면, (b)와 같은 지도가 주어지고 로봇이 (a)와 같은 측정을 했다고 하면 로봇은 (b)의 어두운 영역에 있다고 판단할 것이라는 뜻입니다. 만약 여러분이 (b)와 같은 지도가 주어지고, 시야에는 (a)와 같은 부분만 보인다고 생각해봅시다.
즉, 시야가 5m 정도(위 실제 그림에서 5m는 아니지만 대충 이렇게 가정하겠습니다)로 제한되고, 현재 내 눈에 보이는 것은 앞쪽에는 양쪽으로 문이 두 개가 있으며, 주변을 둘러보며 더 확인하지는 않고 그냥 처음 상태 그대로 있는 것입니다.
그러고 나서 주어진 지도에서 내가 지금 어떤 pose로 있는지 추측해보라고 했을 때, 현재 내 일정 거리 앞에 양쪽으로 문
이 두 개가 있는 곳이라면 전부 다 내가 있을 수 있는 장소가 될 수 있기 때문에 내가 지금 복도의 왼쪽인지 가운데인지 오른쪽인지는 모릅니다. 따라서 그 장소들을 모두 표시한 것이 (b)에서 어두운 부분입니다.
4. Practical Considerations
실제로, 모든 sensor readings의 확률 밀도를 계산하는 것은 계산 관점과 꽤나 관련되어있습니다. 예를 들어, 레이저 거리 스캐너가 한 번의 스캔에 1초가 걸리고, 이때 100개의 값을 리턴한다고 하겠습니다. 우리는 그 스캔의 각각의 빔과 고려되는 가능한 모든 pose에 대해 ray casting operation을 해야 하기 때문에, 그 전체 스캔을 현재의 belief로 전환하는 것의 integration은 항상 실시간으로 처리될 수 없습니다. 이 문제를 해결하기 위한 일반적인 접근방법 중 하나는 각 측정의 일부 부분집합만 처리하는 것입니다(예를 들어, 100번 대신 8번만 측정하는 것입니다.) 이 접근법은 중요한 이점이 있습니다. 거리 스캔에서 인접한 빔들은 보통 독립적이지 않기 때문에, state estimation process는 인접한 측정값에 관련된 noise에 덜 민감하게 됩니다.

예를 들어, 센서가 위 그림과 같이 측정을 한다고 했을 때, 인접한 빔들은 서로 비슷한 값을 가지는 경향이 있습니다. 예를 들어, $d_1$의 빔의 데이터를 알면, 그 바로 옆 빔들의 데이터 또한 어느 정도 비슷할 것이라는 추측이 가능하다는 것입니다. 따라서 각 측정은 완전히 독립적이지는 않다고 볼 수 있습니다.
인접한 측정값의 독립성이 매우 강할 때, ML model은 로봇을 overconfident 하게 할 수도 있고, suboptimal results를 만들어낼 수도 있습니다. 이에 대한 대책은 $p(z_t^k | x_t, m)$을 "weaker" 버전인 $p(z_t^k | x_t, m)^\alpha$로 대체하는 것입니다(이때, $\alpha < 1$ 입니다). 여기서의 직관은 factor $\alpha$에 의해 센서 측정으로부터 추출된 정보를 줄인다는 것입니다.
또 다른 방법은 intrinsic parameters를 응용 분야의 맥락에서 학습하는 것입니다. 예를 들어, mobile localization에서는 좋은 localization을 얻기 위해 multiple time step에 걸쳐 gradient descent를 이용하여 intrinsic parameters를 학습할 수 있습니다.
beam-based model에서 대부분의 computing time을 소비하는 것은 ray casting operation입니다. $p(z_t | x_t, m)$을 계산하는데 걸리는 시간은 ray casting algorithm을 pre-cashing 하는 것과 그 결과를 저장하는 것에 의해 상당히 감소할 수 있고, 그 ray casting operation은 훨씬 더 빠른 table lookup으로 대체될 수 있습니다. 이 아이디어를 적용하는 방법은 state space를 fine-grained three-dimensional grid로 분해하고, 각각의 grid cell에 대해 $z_t^{k*}$를 계산하는 것입니다.
5. Limitations of the Beam Model
beam-based sensor model은 두 가지 단점이 있습니다. 특히, beam-based model은 lack of smoothness를 드러냅니다. 작은 물체들이 많이 모여있는 환경에서, 분포 $p(z_t^k | x_t, m)$은 $x_t$에 대해 매우 unsmooth 합니다. 예를 들어, 많은 책상과 의자가 있는 회의실의 환경을 생각해보면, 이런 환경에서 로봇의 pose $x_t$는 조금만 바뀌어도 센서의 빔의 거리를 조정하는데 매우 큰 영향을 줄 것이라는 것을 알 수 있습니다(장애물이 별로 없는 방을 생각해보면, 로봇의 pose가 바뀐다고 해도 측정값이 크게 달라지지는 않을 것이라는 것도 생각해볼 수 있습니다.)
또 다른 단점은 계산적인 부분입니다. 각 single sensor measurement $p(z_t^k|x_t, m)$을 평가하는 것은 ray casting을 수반하는데, 이는 계산 비용이 큽니다. 위에서 말했듯이, 이 문제는 pose space의 discrete grid 전체에 걸친 범위를 pre-comuting 하는 것으로 일부 해결이 가능합니다. 하지만, 이 결과의 table은 용량이 너무 커서 추가적인 저장 공간을 필요로 하게 됩니다.
'Study > Probabilistic Robotics' 카테고리의 다른 글
| 6.6. Feature-Based Measurement Models (0) | 2020.09.22 |
|---|---|
| 6.4. Likelihood Fields for Range Finders (0) | 2020.09.16 |
| 6. Robot Perception (0) | 2020.09.12 |
| 5.4. Odometry Motion model (0) | 2020.09.10 |
| 5.3. Velocity Motion Model (0) | 2020.09.10 |