이 글은 Sebastian thrun의 Probabilistic Robotics를 보고 내용을 정리한 글이며, 나름 쉽게 표현하기 위해서 의역을 한 부분이 있습니다.
1. 기본 알고리즘(Basic Algorithm)
파티클 필터(particle filter)는 nonparametric 한 베이즈 필터의 실행을 대체하기 위한 방법입니다(parametric 하다는 것은 어떤 모델임을 상정하는 것입니다. 예를 들어 "어떠한 분포가 가우시안 분포를 따를 것이다." 이런 식으로 말입니다. non-paramatic 하다는 것은 반대로 어떤 모델인지 상정하지 않는 것입니다.) 히스토그램 필터처럼, 파티클 필터는 사후 확률을 유한한 숫자의 파라미터들에 의해 근사화합니다. 파티클 필터의 중요한 아이디어는 사후 확률 $bel(x_t)$를 이 사후확률로부터 그려진 랜덤 한 상태 샘플의 집합으로 나타내는 것입니다.

그림 4.3은 가우시안 랜덤변수에 대한 예시입니다. 분포를 parametric 한 형태, 즉 정규 분포를 따르는 지수함수 형태의 확률 밀도 함수로 나타났을 것을, 파티클 필터는 그래프 형태가 아닌, 그 분포로부터 나온 샘플들의 집합의 형태로 나타냅니다. 이러한 표현은 근사적이지만 nonparametric 하며, 따라서 예를 들어 가우시안 같이 더 넓은 공간의 분포도 나타낼 수 있습니다. 또 다른 이점은 랜덤 변수의 비선형 변환도 나타낼 수 있다는 것입니다.
파티클 필터에서 사후확률분포의 샘플들은 "파티클"이라고 하며, 다음과 같이 나타냅니다.

각각의 파티클 $x_t^{[m]} \, ( with\, 1 \leq m \leq M )$ 은 시간 $t$에서의 상태의 구체적인 예시입니다. 다시 말하면, 파티클은 시간 $t$에서 "어떤 것이 '진짜 world의 상태'인가?"에 대한 추측입니다. 여기서 $M$은 파티클 집합 $\chi _t$의 파티클의 개수입니다. 실질적으로, 이 숫자는 보통 1000 이상의 큰 숫자입니다.
이 파티클 필터에 대한 직관은 belief $bel(x_t)$를 파티클 집합인 $\chi _t$로 근사하는 것입니다. 이상적으로, 상태 추측(state hypothesis) $x_t$는 베이즈 필터 사후 확률 $bel(x_t)$에 비례하여 파티클 집합 $\chi _t$에 포함되어야 할 것입니다. 즉,

식 (4.23)의 결과로써, 샘플에 의해 만들어진 상태 공간의 부분 구역의 확률밀도가 높을수록, true state가 그 부분 구역에 있을 확률이 더 높아집니다.
다른 베이즈 필터 알고리즘처럼, 파티클 필터 알고리즘은 1 타임 스텝 빠른 belief인 $bel(x_{t-1})$로부터 재귀적으로 $bel(x_t)$를 만들어냅니다. belief는 파티클의 집합에 의해 나타내어지므로, 이 것은 파티클 필터 집합 $\chi _t$가 집합 $\chi _{t-1}$로부터 만들어진다는 것을 의미합니다.
파티클 필터의가장 기본적인 알고리즘은 Table 4.3에 나타나 있습니다.

알고리즘의 입력값은 파티클 집합 $\chi _{t-1}$와 컨트롤 $u_t$, 가장 최근의 측정값 $z_t$입니다. 다음으로 이 알고리즘은 가장 먼저 $\overline{bel}(x_t)$를 나타내는 임시 파티클 집합 $\chi$를 만듭니다. 이는 입력 집합 $\chi _{t-1}$의 파티클을 조직적으로 처리함으로써 진행됩니다. 다음으로, 이 파티클을 사후 확률 분포 $bel(x_t)$를 근사한 집합 $\chi _t$로 변환하며, 자세한 과정은 아래와 같습니다.
1. Line 4는 $x_{t-1}^{[m]}$과 컨트롤 $u_t$에 기반하며, 시간 $t$일때의 가상 상태(hypothetical state) $x_t^{[m]}$를 만듭니다. 이에 대한 결과 샘플은 $\chi _{t-1}$의 $m$번째 파티클임을 뜻하는 $m$으로 인덱싱 합니다. 이 단계는 상태 과도 분포(state transition distribution) $p(x_t | u_t , x_{t-1})$에서부터 샘플링하는 것을 포함합니다. 여기서 $M$번의 반복 후 얻어진 파티클 집합은 $\overline{bel}(x_t)$를 나타냅니다.
2. Line 5는 각각의 파티클 $x_t^{[m]}$에 대해 $w_t^{[m]}$라고 나타내고 importance factor 라고 하는 값을 계산합니다. importance factor는 측정값 $z_t$를 파티클 집합에 포함하기 위해 사용됩니다. 그러므로, 그 importance는 파티클 $x_t^{[m]}$이 주어졌을 때의 측정값 $z_t$의 확률이며, $w_t^{[m]}$이라고 나타냅니다. 만약 우리가 $w_t^{[m]}$를 파티클의 가중치로써 이해한다면, 근사화된 값에서 가중치가 적용된 파티클은 베이즈 필터 사후 확률 $bel(x_t)$를 나타냅니다.
3. 파티클 필터의 진짜 "기술"은 line 8부터 11입니다. Line 8~11은 리샘플링 또는 중요도 샘플링 이라고 하는 것을 적용합니다. 이 알고리즘은 집합 $\overline{\chi}_t$를 대체한 $M$개의 파티클을 그립니다. 그려진 각 파티클의 확률은 그 파티클의 중요도 가중치(importance weight)로 주어집니다. 리샘플링은 $M$개의 파티클 중 하나의 파티클 집합을 같은 크기의 다른 파티클 집합으로 변환합니다. 리샘플링 처리에 중요도 가중치를 적용함으로써 파티클의 분포는 바뀌게 됩니다. 리샘플링 단계 이전에 파티클은 $\overline{bel}(x_t)$를 따라 분포되었지만, 리샘플링 후 파티클은 사후 확률 $bel(x_t) = \eta p(z_t | x_t^{[m]})\overline{bel}(x_t)$를 따라(근사적으로) 분포하게 됩니다. 더 중요한 점은 $\chi _t$에 포함되지 않은 파티클인데, 이 파티클은 낮은 중요도 가중치를 갖는 경향이 있습니다.
2. 중요도 샘플링(Importance Sampling)
직관적으로, 우리는 확률밀도함수 $f$를 계산해야 하는 문제에 직면해 있습니다. 하지만 우리는 단지 다른 확률 밀도 함수 $g$에 의해 주어진 샘플만 알고 있습니다. 예를 들어, 우리는 $x \in A$인 $x$의 기댓값(expectation)에 대해 관심이 있다고 하겠습니다. 우리는 이 확률을 $g$에 대한 기댓값으로 나타낼 수 있습니다. 다음 식에서 $I$는 매개변수가 참이면 1이고, 아니면 0인 지시함수(indicator function)이라고 하겠습니다.

여기서 $w(x) = \frac{f(x)}{g(x)}$는 $f$와 $g$의 불일치(mismatch)를 나타내는 가중치 요소(weighting factor)입니다. 이 방정식이 성립하기 위해, $f(x) > 0\rightarrow g(x) > 0$이어야 합니다.
중요도 샘플링은 위의 변환을 이용합니다. 그림 4.4의 a는 $f$의 확률 밀도 분포를 보여주며, 이는 target distribution이라고 합니다. 이전에, 우리가 얻으려고 한 것은 바로 이 $f$로부터의 샘플이었습니다. 하지만, $f$에서 직접적으로 샘플링을 하는 것은 거의 불가능합니다. 따라서 우리는 그 대신에 그림 4.4의 b에 있는 $g$의 확률 밀도로부터 파티클을 생성합니다.
즉, 우리가 얻고싶은 것은 그림 4.4의 (a)와 같은 그래프입니다. (a)에서 그림 밑쪽의 파티클을 통해 밀도추출을 하면 $f$와 같은 그래프의 추정이 가능한데, 이와 같은 파티클을 확률적으로 샘플하는 것이 불가능합니다. 확률적으로 샘플링 하는 것은 특정한 분포를 따라야 가능합니다. 따라서 (b)에서의 $g$의 그래프로부터의 파티클을 이용하여 (c)와 같이 가중치를 적용한 파티클의 결과를 통해 $f$를 어느정도 비슷하게 추정할 수 있습니다.

여기서 확률 밀도 $g$에 대응되는 분포는 proposal distribution이라고 합니다. 확률 밀도 $g$는 $f(x) > 0$인 것처럼 $g(x) > 0$이어야 하며, 따라서 최종적으로 $f$에서의 샘플링에 의해 얻어질 상태를 위해 $g$에서 샘플링을 할 때, 확률이 0인 파티클은 없습니다. 그림 4.4의 (b)의 아래쪽에서 파티클 집합의 결과들은 $f$가 아닌 $g$의 분포를 따르고 있습니다. 어떠한 구간 $A\subseteq \tt dom(\it X\tt)$에서 실증적인 $A$의 영역 안의 파티클 숫자는 $g$의 구간 $A$에 대한 적분 값으로 수렴합니다.

$f$와 $g$사이의 차이를 offset 하기 위해, 파티클 $x^{[m]}$은 아래 값에 의해 가중됩니다.

이 것은 그림 4.4.의 (c)에 나와있습니다. 이 그림에서의 수직선들은 중요도 가중치(importance weight)의 크기를 나타냅니다. 중요도 가중치들은 아직 각각 파티클의 확률 질량 함수를 정규화(normalize) 하지 않았습니다.

위 식에서 첫번째 항은 모든 중요도 가중치를 위한 정규화 상수(normalizer)입니다. 다시 말해, 우리가 확률 밀도 $g$로부터 파티클들을 생성했을지라도, 적절하게 가중된 파티클들은 확률 밀도 $f$로 수렴한다는 것입니다. 이 것은 가벼운 조건 하에서 보일 수 있는데, 이 근사는 임의의 집합 $A$에 대해 우리가 요구하는 $E_f[I(x\in A)]$로 수렴합니다. 대부분의 경우에서, convergence의 비율은 $O(\frac{1}{\sqrt{M}})$이며, 여기서 $M$은 샘플의 개수입니다. constant factor는 $f$와 $g$가 얼마나 유사한지(similarity)에 의존합니다.
파티클 필터에서, 확률 밀도 $f$는 target belief $bel(x_t)$에 대응됩니다. (점근적으로 조정하는) 가정 하에 $\chi _{t-1}$의 파티클들은 $bel(x_{t-1})$을 따라 분포되며, 확률 밀도 $g$는 아래 식과 같은 확률 곱에 대응됩니다.
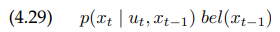
다시 말하지만, 이 분포는 proposal distribution이라고 합니다.
3. 파티클 필터의 실질적 고려사항과 속성(Parctical Considerations and Properties of Particle Filters)
밀도 추출(Density Extraction)
파티클 필터에 의해 유지되는 샘플 집합은 연속적 belief의 불연속 근사를 나타냅니다. 하지만, 많은 응용분야에서 연속적인 추정의 가능을 요구하며, 이 추정은 파티클에 의해 나타내어진 어떤 특정 상태에서만의 추정이 아니라 상태 공간 내부의 어떠한 지점에서도 가능해야 합니다. 이런 샘플에서 연속적인 확률 밀도를 추출(extract)하는 문제를 밀도 추정(density estimation)이라고 합니다(밀도 추정에 대한 자세한 설명은 darkpgmr.tistory.com/147 를 참조하세요).
그림 4.5는 파티클로부터 밀도를 추출하는 여러 방법들을 보여줍니다.

(a)는 변환된 가우시안의 파티클과 확률 밀도 함수입니다. 이런 파티클에 대해 간단하고 매우 효과적인 밀도 추정 접근법으로는 가우시안 근사가 있으며, 이는 그림 4.5의 (b)에 나타냈습니다. 이 경우, 파티클로부터 추출된 가우시안 그래프는 true density의 가우시안 근사와 가상적으로 같습니다(virtually identical).
분명히, 가우시안 근사는 확률 밀도 함수의 기본적인 속성만을 잡아내고, 그 확률 밀도 함수가 단봉형(unimodal)인 경우에만 적절합니다. 다봉 형(multimodal) 샘플 분포는 k-평균 클러스터링(k-means clustering)같이 더 복잡한 테크닉을 필요로 합니다. 이에 대한 또 다른 접근법은 그림 4.5의 (c)에 나타내었습니다. 여기 나타난 불연속 히스토그램은 상태 공간(state space)과 이 범위 안의 파티클들의 가중치를 더하여 계산한 각각의 bin의 확률을 겹쳐놓았습니다.
커널 밀도 추정은 파티클 집합을 연속 확률 밀도로 바꿔주는 다른 방법입니다. 여기서 각각의 파티클들은 커널의 중심 값으로 사용되고, 전체적인 확률 밀도는 이 커널 밀도의 혼합에 의해 주어집니다(위에서 언급한 링크를 참조하세요). 커널 밀도 추정의 장점은 smoothness와 간단한 알고리즘입니다. 하지만, 어떠한 점에서의 확률 밀도를 계산하는것의 계산 복잡도는 파티클 또는 커널의 개수에 선형적으로 비례합니다.
많은 로보틱스 응용분야에서는 컴퓨팅 파워가 매우 제한되어있고 파티클의 평균은 로봇을 컨트롤 하기에 충분한 정보를 제공해줍니다. active localization같은 경우, 상태 공간에서의 불확실성에 대한 정보처럼 더 복잡한 정보에 의존합니다. 이런 상황의 경우, 히스토그램이나 가우시안의 혼합이 더 적절합니다. 여러 로봇에 의해 수집된 데이터를 조합하는 경우에는 다른 샘플 집합의 확률 밀도들을 곱하는 것을 요구하기도 합니다. 이런 경우에는 density tree나 커널 밀도 추정이 더 적합합니다.
Sampling Variance
파티클 필터에서의 오류의 중요한 원인 중 하나는 랜덤 샘플링에 내재하는 분산에 관련되어 있습니다. 확률 밀도로부터 유한한 개수의 샘플이 그려질 때마다, 이 샘플로부터 추출된 통계는 원래 확률 밀도의 통계와는 조금씩 다릅니다. 예를 들어, 우리가 만약 가우시안 랜덤 변수로부터 샘플을 그리면, 그 평균과 분산은 원래의 랜덤 변수와는 다를 것입니다.
가우시안 belief가 같고, 노이즈가 없는 두 개의 같은 로봇이 움직인다고 상상해보겠습니다. 분명히, 두 로봇은 같은 행동을 하고 나서는 같은 belief를 가져야 할 것입니다. 이 상황을 시뮬레이션하기 위해, 가우시안 확률 분포와 그 값을 비선형 변환시킨 값에 의한 샘플들을 반복해서 그리겠습니다. 그림 4.6은 그 결과 샘플 및 커널 밀도 추정과 함께 true belief(회색 영역)을 보여줍니다.

왼쪽 열의 각각의 그래프들은 가우시안으로부터 그려진 25개의 샘플에 대한 결과를 보여줍니다. 우리가 요구하는 결과와 다르게, 일부 커널 밀도 추정은 true density와는 상당히 다를 뿐 아니라 각 실험에 대한 차이도 매우 큽니다. 그러나 샘플의 숫자가 많아지면 샘플링 분산은 줄어들게 됩니다. 위 그림에서 볼 수 있듯이 오른쪽 열은 250개의 샘플에 대한 일반적인 결과를 보여줍니다. 위 그래프는 샘플의 숫자가 많기 때문에 분산이 줄어들고 더 정확하게 근사하는 결과를 보여줍니다. 실제로, 충분한 개수의 샘플이 선택되면 로봇에 의한 관측은 일반적으로 true belief에 "충분히 근접한" belief에 근거한 샘플들을 유지(keep)합니다.
리샘플링(Resampling)
샘플링 분산은 반복적인 리샘플링을 통해 증폭됩니다. 이 문제를 이해하기 위해, 극단적인 경우를 생각하면 도움이 되는데, 예를 들어 로봇의 상태가 변하지 않는 경우를 생각해보겠습니다. 즉, 로봇의 상태 $x_t = x_{t-1}$이고 로봇의 위치 추정(localization)이 움직이지 않는 예시입니다. 여기서 추가적으로 로봇이 아무 센서도 가지고 있지 않다고 가정하겠습니다. 따라서, 로봇은 상태를 추정할 수 없고, 상태에 대해 알 수도 없습니다. 분명히, 로봇은 자신의 위치에 대해 아무 정보도 얻을 수 없기 때문에 시간 $t$에서의 추정은 시간 $t$에서의 어떠한 지점에서도 초기의 추정 값과 같아야 합니다.
초기에, 파티클은 사전확률로부터 만들어질 것이며, 이 파티클들은 상태 공간에 퍼져있을 것입니다. 하지만, 리샘플링 단계(알고리즘의 line 8)는 상태 샘플 $x^{[m]}$을 다시 만들어내는데 때때로 실패할 것입니다. 이는 상태 과도(state transition)가 결정적(deterministic)이어서 어떠한 새로운 상태도 이전의 샘플링 단계(line 4)에서 사용되지 않기 때문입니다($x_t = x_{t-1}$이기 때문에 이전 상태를 알면 현재 상태는 이전 상태에 따른 확률이 1이 되고 다른 상태의 확률은 0이 될 것입니다).
시간이 지남에 따라, 리샘플링 단계의 랜덤한 성질로 인해 더 많은 파티클들이 새로운 파티클을 만들지 않고 그냥 지워지게 됩니다. 즉, 한 개의 확률, 어떤 한 개의 파티클과 같은 $M$개의 복사본만 살아남을 것입니다. 즉, 반복되는 리샘플링으로 인해 다양성이 사라지게 될 것입니다. 바깥의 관측자가 보기에는 이 것은 로봇이 유일한 world state를 유일하게 갖게 되는 것으로 보일 수 있습니다. 이는 로봇이 센서가 없다는 것에 대해 분명한 모순입니다.
이 예제는 중요한 실질적 영향과 함께 파티클 필터의 다른 한계에서의 힌트를 줍니다. 특히, 리샘플링 처리는 파티클 생성에 있어 다양성을 감소키며, 스스로 근사 오차로써 분명해지게 됩니다. 즉, 파티클 집합 자체의 분산은 감소될지라도, true belief를 추정하는데 있어서 파티클 집합의 분산은 증가하게 됩니다. 파티클 필터의 분산, 오차를 제어하는 것은 어떠한 실질적 적용에서든지 필수적입니다.
이 분산을 줄이기 위해서 2개의 주요 접근법이 있습니다. 첫 번째 방법은 리샘플링의 주파수를 줄이는 것입니다. 만약 상태가 정적이라고($x_t = x_{t-1}$) 알려지면, 이에 대한 리샘플링은 실행되지 않을 것입니다. 예를 들어 이런 경우, 모바일 로봇의 위치추정에서는 로봇이 멈출 때, 리샘플링은 중단되어야 합니다. 만약 상태가 바뀐다고 하더라도, 이 것은 리샘플링의 주파수를 줄이기 위한 좋은 방법입니다. 여러 측정값들은 위에서 설명했듯이 곱해가며 importance factor를 업데이트하는 것을 통해 합쳐질 수 있습니다. 구체적으로, 업데이트는 다음과 같이 이루어집니다.
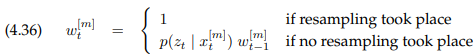
리샘플링을 언제 해야하는지의 선택은 복잡하고, 실질적인 경험을 필요로 합니다. 너무 자주 리샘플링을 하면 다양성을 잃을 위험이 있고, 만약 샘플링을 너무 적게 하면 확률이 작은 영역의 샘플이 낭비될 수 있습니다. 리샘플링을 해야 하는지 결정하는 기본적인 접근법은 중요도 가중치의 분산을 측정하는 것입니다. 가중치의 분산은 샘플에 기반한 표현의 효율성에 관련됩니다. 만약 모든 가중치가 같다면, 그 분산은 0이고 리샘플링은 실행되지 않을 것입니다. 반면, 적은 숫자의 샘플에 가중치가 집중되어있다면, 가중치 분산은 높을 것이고 리샘플링이 실행될 것입니다.
샘플링 에러를 줄이기 위한 두 번째 전략은 low variance sampling이라고 합니다. table 4.4는 low variance sampling을 나타냅니다.

기본적인 아이디어는 다른 리샘플링 처리에 대해 독립적으로 샘플을 선택하는 대신, 순차적인 확률적 처리(sequential stochastic process)를 포함하여 선택하는 것입니다. $M$개의 랜덤한 숫자와 그 숫자에 대응하는 파티클들을 선택하는 대신, 이 알고리즘은 하나의 랜덤한 숫자를 계산하고, 이 숫자에 따라서 샘플들을 선택하지만, 그 샘플을 선택할 확률은 여전히 샘플의 가중치에 비례합니다. 이 것은 구간 $\left[0;M^{-1}\right]$에서의 랜덤 한 숫자 $r$을 선택하는 것에 의해 실행됩니다. 여기서 $M$은 시간 $t$에 그려진 샘플의 수입니다. 다음으로, 알고리즘은 파티클을 선택할 때, 반복하여 고정된 수 $M^{-1}$을 $r$에 더하고, 그 결과의 수에 대응되는 파티클을 선택합니다. 구간 $\left[0;1\right]$에서의 어떤 숫자 $U$는 정확히 하나의 파티클을 가리키는데, 그 파티클 $i$는 아래와 같이 정의됩니다.

Table 4.4의 while문은 방정식의 우항의 합을 계산하며, 추가적으로 $i$가 가중치의 합이 처음으로 $U$를 초과하는 첫 번째 파티클의 인덱스인지 확인합니다. 이 선택은 line 12에서 구현하였습니다. 이 과정을 나타내는 그림은 그림 4.7에 나타내었습니다.

위 그림을 좀더 설명하자면, $\left[0;M^{-1}\right]$에서의 어떤 작은 수 $r$을 선택하고, 우리가 원하는 샘플의 수 M개만큼 일정한 간격으로 샘플링을 합니다. 그림에서 보시다시피 가중치가 클수록 더 많이 샘플링되고, 가중치가 작을수록 더 적게 샘플링될 것이라고 추측할 수 있습니다.
좀 더 쉽게 설명하기 위해 구체적인 예시를 들겠습니다.

먼저, line 6의 for문으로 들어갑니다. 여기서 초기의 $c$는 $w_t^{[1]}$인데, 만약 $U$가 이 값을 넘지 않으면 그대로 $x_t^{[1]}$을 $\overline{\chi}_t$에 추가하고, $m$을 1 증가시킵니다. 위 그림의 경우, $m=3$일때 까지 반복하고, $m=4$일때 식 (4.37)의 경우이자 line 8의 상황이 되면서 $i$와 $c$가 증가합니다. 따라서 새로운 상태인 $x_t^{[2]}$가 $\overline{\chi}_t$에 추가되며, 이 과정을 반복하며 샘플링합니다. 따라서 가중치가 클수록 해당 상태에 대응하는 샘플 수가 많아지게 됩니다.
Particle Deprivation
많은 개수의 particles이 사용된다고 하더라도, correct state 주변에 particles이 없는 경우가 발생할 수도 있습니다. 이 문제는 particle deprivation problem이라고 합니다. 이 문제는 대부분 high likelihood를 가진 relevant region을 커버하기에는 particles의 수가 너무 적을 때 발생합니다.
particle deprivation은 random sampling의 분산의 결과로 인해 발생하는데, 즉 운이 없는 랜덤한 숫자들로 인해 true state 주변의 particles들이 없어질 수 있다는 것입니다. 각각의 sampling step에서, 이런 경우가 일어날 확률은 $M$의 크기에 따라 지수적으로 감소하기는 하지만 그래도 0보다는 큽니다. 따라서, 우리는 particle filter를 충분히 길게 실행해야 하지만, 마침내 무작위로 incorrect한 추정의 결과가 나올 수도 있습니다.
실제로, 이런 문제는 high likelihood를 가진 states의 공간에 대해 $M$이 상대적으로 작은 경우에만 발생하는 경향이 있습니다. 이 particle deprivation problem을 해결하기 위한 인기있는 솔루션은 particles를 각각 resampling process가 끝난 후에, 실제 motion이나 measurement commands에 상관 없이 작은 숫자의 랜덤한 particles를 추가하는 것입니다. 이런 방법은 deprivation problem을 줄일 수 있지만, incorrect posterior estimate의 비용적 측면에서는 그렇지 못합니다.
'Study > Probabilistic Robotics' 카테고리의 다른 글
| 5.4. Odometry Motion model (0) | 2020.09.10 |
|---|---|
| 5.3. Velocity Motion Model (0) | 2020.09.10 |
| 3.3 The Extended Kalman Filter (0) | 2020.09.10 |
| 3.2 The Kalman Filter (0) | 2020.09.10 |
| 2.4. Bayes Filters (0) | 2020.09.10 |