이 포스트는 Do it! 정직하게 코딩하며 배우는 딥러닝 입문 pp.197~231를 참고하였습니다.
여러 개의 이미지를 분류하는 다층 신경망 만들기
이진 분류에서는 다음과 같은 다층 신경망을 사용했습니다. 0.5를 기준으로 해서 출력층의 활성화 값이 이보다 크면 양성, 작으면 음성으로 분류했습니다.

다중 분류를 위한 신경망을 구하는 방법은 위의 구조에서 출력층의 개수만 추가하면 됩니다. 이진 분류와 다중 분류를 위한 신경망의 구조를 비교해보면, 출력층의 개수만 다릅니다. 이진 분류는 양성 클래스에 대한 확률 $\hat{y}$ 하나만 출력하지만, 다중 분류는 각 클래스에 대한 확률을 출력합니다. 예를 들어 클래스가 3개라면 $\hat{y}_1, \hat{y}_2, \hat{y}_3$ 이렇게 3개의 출력이 나옵니다. 이를 위해 다중 분류 신경망은 출력층에 분류할 클래스 개수만큼의 뉴런을 배치합니다.
다중 분류의 문제점과 소프트맥스 함수
다음은 클래스를 분류하는 다중 분류 신경망의 출력층을 확인해 본 것입니다.

왼쪽과 오른쪽 모두 해당 샘플이 자동차일 확률이 제일 높다고 예측합니다. 하지만, 왼쪽 출력의 값을 보면 모든 값이 대체로 높은데 그 중에서 자동차일 확률이 더 높은 것이고, 오른쪽 출력은 대체로 값이 낮지만 자동차일 확률이 상대적으로 더 높습니다.
위의 두 출력을 비교해보면, 오른쪽의 신경망이 더 잘 예측한 것이라고 볼 수 있습니다. 언뜻 보기에는 감이 잘 오지 않을 수 있는데, 이는 출력의 합이 같지 않기 때문에 비교하기 어려운 것입니다. 따라서, 소프트맥스 함수를 적용해 출력 강도를 정규화 해서 비교해봐야 합니다. 여기서 출력 강도를 정규화한다는 것은 전체 출력의 합을 1로 만드는 것입니다.
출력이 $n$개인 다중 분류 신경망에서 해당 샘플이 $i$번째 클래스일 확률을 나타내는 소프트맥스 함수는 다음과 같습니다.
$\frac{e^{z_i}}{\sum_{k=1}^n e^{z_k}}$
여기서 $e^{zi}$는 각 층의 선형 출력을 의미합니다. 이제, 위 그림에서 두 신경망의 결과를 소프트맥스 함수에 적용해보겠습니다.
시그모이드 함수 공식은 $\hat{y} = \frac{1}{1+e^{-z}}$이므로, 이를 $z$에 대해 정리하면 $z=-\ln{(\frac{1}{\hat{y}}-1)}$이 됩니다. 따라서, 왼쪽 그림의 출력값들을 대입하여 $z$를 구한 결과는 다음과 같습니다.

위 값을 소프트맥스 함수에 적용하면 아래와 같이 정규화된 값을 얻을 수 있습니다.

이번에는 오른쪽 그림의 결과입니다.

이제 두 출력의 결과를 제대로 비교할 수 있습니다. 신경망에서의 소프트맥스 함수는 다음과 같이 표현할 수 있습니다.

이진 분류에서는 로지스틱 손실 함수를 사용했었습니다. 다중 분류에서는 로지스틱 함수의 일반화 버전인 크로스 엔트로피(cross entropy) 손실 함수를 사용합니다.
크로스 엔트로피 손실 함수
정보 이론에서 사용하는 엔트로피의 정의는 다음과 같습니다.
$H(x) = -\sum_xp(x)\log p(x)$
이는 정보의 불확실성을 나타냅니다. 엔트로피가 높다는 것은 정보가 많고, 확률이 낮다는 뜻입니다.
정보이론에서 확률이 매우 높거나 매우 낮은 것, 즉 확실한 것은 정보가 아닙니다. 예를 들어보겠습니다. 정확한 비유는 아니겠지만, 저의 직관은 이렇습니다.
내일 지구가 파괴될 확률이 0%인데, 이에 대해 아는 것은 정보가 아닙니다. 어차피 확실한 것이거든요. 내일 지구가 파괴되지 않을 확률이 100%라는 것도 마찬가지입니다. 하지만 내일 비가 올 확률이 50%인데 이에 대한 정보를 안다면 이는 매우 큰 정보라고 볼 수 있습니다. 따라서 엔트로피의 그래프를 보면 다음과 같습니다.

크로스 엔트로피는 다음과 같이 정의됩니다.
$CE(p, q) = -\sum_x p(x)\log q(x)$
실제 분포 $p$가 있고, 우리가 모델링한 분포 $q$가 있는 상황입니다. 위 값은 여기서 우리가 모델링한 $q$가 얼마나 $p$와 비슷한가를 나타낸다고 보시면 됩니다. 이 값은 두 분포의 차이를 나타냅니다. 두 분포가 비슷하면 차이가 없기 때문에 그냥 엔트로피에 가까운 값이 나오고, 두 분포의 차이가 크면 값이 커집니다.
이제 이를 머신러닝에 적용해봅니다. 머신러닝의 원래 목표는 '실제 분포를 따라하는 것' 이라고 볼 수 있습니다. 신경망을 통해 실제 분포와 비슷한 분포를 만들어내는 것입니다.
보통 두 분포간의 차이를 얘기할 때는 Kullback-Leibler divergence(KL divergence)라는 식을 사용하며, 이는 다음과 같이 정의됩니다. 두 분포가 같으면 0이되고, 차이가 클 수록 값이 커집니다.
$D_{KL}(p||q) = \sum_x p(x)\log\frac{p(x)}{q(x)}$
위 식을 조금 바꿔서 표현해보면 다음과 같습니다.
$D_{KL}(p||q) = \sum_x p(x)\log\frac{p(x)}{q(x)}$
$= \sum_x p(x)\log p(x) - \sum_x p(x)\log q(x)$
$= -H(p) + CE(p, q)$
분류 문제에서, 우리가 원하는 분포 p는 다음과 같습니다.
$P(X = k) = 1$
$P(X = c) = 0 \; ( c\neq 1)$
즉, 정답 클래스가 k이고 나머지 클래스들은 정답이 아닌 분류 문제에서, $X$가 k라는 클래스로 분류될 확률이 1을 갖고 나머지는 전부 0의 값을 갖는것이 완벽한 분류기이기 때문에, 바로 이 분포가 우리가 원하는 분포입니다. 이런 분포의 경우에는 엔트로피의 값이 0이 되기 때문입니다.
$H(X) = -\sum_{c=1}^C P(X=c)\log P(X=c)$
$= -P(X=1)\log P(X=1)$
$= -1\log 1 $
$= 0$
아까 KL divergence에서 지금과 같이 엔트로피에 0을 대입하면, KL divergence는 그냥 크로스엔트로피가 됩니다. 즉, 우리가 원하는 분포 p와 예측 분포 q가 비슷해질수록 크로스엔트로피는 값이 작아지겠네요. 즉, 크로스엔트로피 값이 작으면 우리가 원하는 분포에 가깝다는 뜻입니다.
따라서, 크로스엔트로피를 손실 함수로 선택하여 최소화하면 될 것 같습니다. 이에 대한 자세한 내용은 링크를 참조하세요.
이제, 크로스 엔트로피 손실 함수를 보겠습니다.
$L = -\sum_{c=1}^C y_c\log(a_c) = -(y_1\log(a_1)+y_2\log(a_2)+\dots+y_c\log (a_c)) = -\log(a_{y=1})$
위에서 말한 상황과 같습니다. 타깃값, 즉 실제 분포 $y$가 있고, 우리가 모델링한 분포 $a$가 이를 얼마나 잘 따라했는가를 나타내네요. 그런데 위 식에서, 타깃의 값은 1이고, 나머지는 전부 0이므로 타깃이 되는 특정 $y$에 해당되는 $a$값만 빼고 나머지는 전부 없애면 되겠네요. 따라서 손실함수는 다음과 같습니다.
$y = \begin{cases}-\log a & (positive\;class)\\ -\log (1-a) & (negative\;class)\end{cases}$
크로스 엔트로피 손실 함수 미분하기
이제 경사 하강법을 적용하기 위해 크로스 엔트로피 손실 함수도 미분해보겠습니다. 위의 그림과 같이 클래스가 3개인 경우에 대한 크로스 엔트로피를 미분해보겠습니다. 먼저, 손실 함수를 $z_1$에 대해 미분해봅니다. 여기서 중요한 점은 $a_1, a_2, a_3$ 모두 $z_1$에 관한 함수이고, 손실 함수도 $a_1, a_2, a_3$에 관한 함수이므로, 연쇄 법칙은 다음과 같습니다.
$\frac{\partial L}{\partial z_1} = \frac{\partial L}{\partial a_1}\frac{\partial a_1}{\partial z_1}+
\frac{\partial L}{\partial a_2}\frac{\partial a_2}{\partial z_1}+
\frac{\partial L}{\partial a_3}\frac{\partial a_3}{\partial z_1}$

이제, 크로스 엔트로피 손실 함수를 보겠습니다. 위 식의 경우, 손실 함수는 $L = -(y_1\log(a_1)+y_2\log(a_2)+y_3\log(a_3)$입니다. 따라서 이를 미분하면,
$\frac{\partial L}{\partial a_1} = -\frac{\partial}{\partial a_1}(y_1\log(a_1)+y_2\log(a_2)+y_3\log(a_3) = -\frac{y_1}{a_1}$
$\frac{\partial L}{\partial a_2} = -\frac{y_2}{a_2}$
$\frac{\partial L}{\partial a_3} = -\frac{y_2}{a_3}$
이 값을 $\frac{\partial L}{\partial z_1}$에 대입하면 다음과 같습니다.
$\frac{\partial L}{\partial z_1} = \frac{\partial L}{\partial a_1}\frac{\partial a_1}{\partial z_1}+
\frac{\partial L}{\partial a_2}\frac{\partial a_2}{\partial z_1}+
\frac{\partial L}{\partial a_3}\frac{\partial a_3}{\partial z_1}
= (-\frac{y_1}{a_1})\frac{\partial a_1}{\partial z_1}
+ (-\frac{y_2}{a_2})\frac{\partial a_2}{\partial z_1}
+(-\frac{y_3}{a_3})\frac{\partial a_3}{\partial z_1}$
다음으로는 $\frac{\partial a_1}{\partial z_1}$을 구해보겠습니다.


같은 방식으로 나머지 값에 대해서도 미분하면 다음과 같습니다.

이제 위에서 구한 값들을 사용하면 $L$의 $z_1$에 대한 미분값을 구할 수 있습니다.

위 식에서 $y_1 + y_2 + y_3$는 타깃 값의 합인데, 정답 타깃은 1이고 나머지는 0이므로 이 값은 항상 1입니다. 최종적으로, 크로스 엔트로피 손실 함수를 미분해서 $frac{\partial L}{\partial z_1} = -(y_1 - a_1)$임을 알았습니다. 이와 같은 방식으로 $z_2, z_3$에 대해서도 크로스 엔트로피 손실 함수를 미분하면 $-(y_2 - a_2), -(y_3 - a_3)$이므로, 최종적으로 다음과 같은 값을 얻을 수 있습니다.
$\frac{\partial \pmb{L}}{\partial \pmb{z}} = -(\pmb{y-a})$
위 결과를 보니, 로지스틱 손실 함수의 미분과 결과가 같습니다. 따라서, 크로스 엔트로피 손실 함수를 역전파에 사용할 때, 이 부분을 따로 수정할 필요가 없을 것 같습니다.
다중 분류 신경망 구현하기
이전 포스트에서 사용했던 MinibatchNetwork 클래스를 확장할 것입니다. 전체 코드는 다음과 같습니다.
import numpy as np
class MultiClassNetwork:
def __init__(self, units=10, batch_size=32, learning_rate=0.1, l1=0, l2=0):
self.units = units
self.batch_size = batch_size
self.w1 = None
self.w2 = None
self.b1 = None
self.b2 = None
self.a1 = None
self.losses = []
self.val_losses = []
self.lr = learning_rate
self.l1 = l1
self.l2 = l2
def sigmoid(self, z):
a = 1 / (1 + np.exp(-z))
return a
def softmax(self, z):
exp_z = np.exp(z)
return exp_z / np.sum(exp_z, axis=1).reshape(-1, 1)
def init_weights(self, n_features, n_classes):
self.w1 = np.random.normal(0, 1, (n_features, self.units))
self.w2 = np.random.normal(0, 1, (self.units, n_classes))
self.b1 = np.zeros(self.units)
self.b2 = np.zeros(n_classes)
def predict(self, x):
z = self.forpass(x)
return np.argmax(z, axis=1)
def score(self, x, y):
return np.mean(self.predict(x) == np.argmax(y, axis=1))
def reg_loss(self):
return self.l1*(np.sum(np.abs(self.w1)) + np.sum(np.abs(self.w2))) + \
self.l2/2 * (np.sum(self.w1**2) + np.sum(self.w2**2))
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val)
a = self.softmax(z)
a = np.clip(a, 1e-10, 1-1e-10)
val_loss = -np.sum(y_val*np.log(a))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val))
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1
self.a1 = self.sigmoid(z1)
z2 = np.dot(self.a1, self.w2) + self.b2
return z2
def backprop(self, x, err):
m = len(x)
w2_grad = np.dot(self.a1.T, -err) / m
b2_grad = np.sum(-err) / m
err_to_hidden = np.dot(-err, self.w2.T) * self.a1 * (1 - self.a1)
w1_grad = np.dot(x.T, err_to_hidden) / m
b1_grad = np.sum(err_to_hidden, axis=0) / m
return w1_grad, b1_grad, w2_grad, b2_grad
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
np.random.seed(42)
self.init_weights(x.shape[1], y.shape[1])
for _ in range(epochs):
loss = 0
print('.', end='')
for x_batch, y_batch in self.gen_batch(x, y):
a = self.training(x_batch, y_batch)
a = np.clip(a, 1e-10, 1-1e-10)
loss += np.sum(-y_batch*np.log(a))
self.losses.append((loss + self.reg_loss()) / len(x))
self.update_val_loss(x_val, y_val)
def gen_batch(self, x, y):
length = len(x)
bins = length // self.batch_size
if length % self.batch_size:
bins += 1
indexes = np.random.permutation(np.arange(len(x)))
x = x[indexes]
y = y[indexes]
for i in range(bins):
start = self.batch_size*i
end = self.batch_size*(i+1)
yield x[start:end], y[start:end]
def training(self, x, y):
m = len(x)
z = self.forpass(x)
a = self.softmax(z)
err = y - a
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
w1_grad += (self.l1*np.sign(self.w1) + self.l2*self.w1) / m
w2_grad += (self.l1*np.sign(self.w2) + self.l2*self.w2) / m
self.w1 -= self.lr*w1_grad
self.w2 -= self.lr*w2_grad
self.b1 -= self.lr*b1_grad
self.b2 -= self.lr*b2_grad
return a
1. 소프트맥스 함수 추가하기
def sigmoid(self, z):
a = 1 / (1 + np.exp(-z))
return a
def softmax(self, z):
exp_z = np.exp(z)
return exp_z / np.sum(exp_z, axis=1).reshape(-1, 1)
소프트맥스 함수에서 np.sum()함수를 사용한 부분을 그림으로 나타내면 다음과 같습니다.
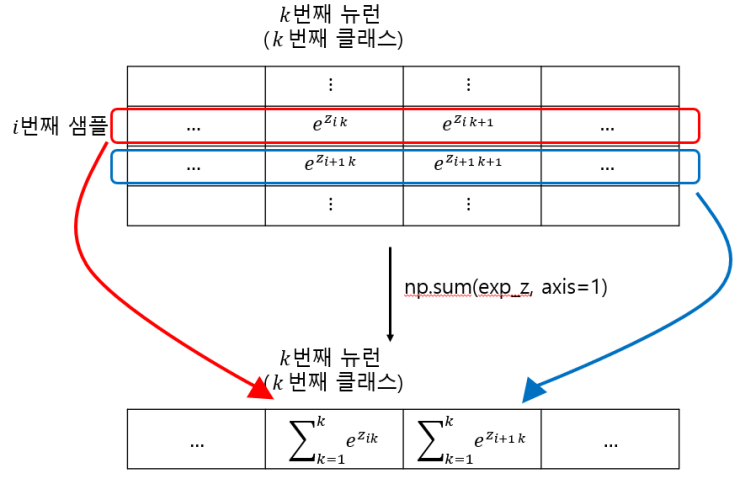
np.sum()함수를 사용하면 리턴값이 행벡터 형태로 나오므로, 이를 다시 열벡터 형태로 바꿔서 원래 행렬에서 나눠줘야 각 클래스별로 확률이 구해진, 우리가 원하는 소프트맥스 함수의 결과를 얻을 수 있습니다.

2. 정방향 계산하기
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1
self.a1 = self.sigmoid(z1)
z2 = np.dot(self.a1, self.w2) + self.b2
return z2활성화 함수를 sigmoid()로 바꿨으니 여기서도 바꿔줘야합니다.
3. 가중치 초기화하기
def init_weights(self, n_features, n_classes):
self.w1 = np.random.normal(0, 1, (n_features, self.units))
self.w2 = np.random.normal(0, 1, (self.units, n_classes))
self.b1 = np.zeros(self.units)
self.b2 = np.zeros(n_classes)이진 분류에서는 출력층의 뉴런이 1개였으므로, $\pmb{W}_2$의 크기가 (은닉층의 뉴런 수 X 1)이었지만, 이제 출력층의 뉴런 수가 우리가 분류 할 개수 만큼 늘었으므로, (은닉층의 뉴런 수 X 클래스 개수)가 됩니다.
4. fit() 메서드 수정하기
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
np.random.seed(42)
self.init_weights(x.shape[1], y.shape[1])
for _ in range(epochs):
loss = 0
print('.', end='')
for x_batch, y_batch in self.gen_batch(x, y):
a = self.training(x_batch, y_batch)
a = np.clip(a, 1e-10, 1-1e-10)
loss += np.sum(-y_batch*np.log(a))
self.losses.append((loss + self.reg_loss()) / len(x))
self.update_val_loss(x_val, y_val)훈련의 상황을 확인할 수 있도록 에포크 마다 '.'이 출력되게 합니다.
5. training() 메서드 수정하기
def training(self, x, y):
m = len(x)
z = self.forpass(x)
a = self.softmax(z)
err = y - a
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
w1_grad += (self.l1*np.sign(self.w1) + self.l2*self.w1) / m
w2_grad += (self.l1*np.sign(self.w2) + self.l2*self.w2) / m
self.w1 -= self.lr*w1_grad
self.w2 -= self.lr*w2_grad
self.b1 -= self.lr*b1_grad
self.b2 -= self.lr*b2_grad
return a활성화 함수의 이름을 바꿨으므로, 이에 맞게 호출하는 함수의 이름을 바꿉니다.
6. predict() 메서드 수정하기
def predict(self, x):
z = self.forpass(x)
return np.argmax(z, axis=1)정방향 계산에서 얻은 출력 중 가장 큰 값이 예측값입니다. 예측 확률 값 자체를 구하고 싶다면 소프트맥스 함수를 통과해야 하지만, 클래스의 예측값만 확인하려면 소프트맥스 함수를 적용하지 않아도 됩니다.
7. score() 메서드 수정하기
def score(self, x, y):
return np.mean(self.predict(x) == np.argmax(y, axis=1))
8. 검증 손실 계산하기
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val)
a = self.softmax(z)
a = np.clip(a, 1e-10, 1-1e-10)
val_loss = -np.sum(y_val*np.log(a))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val))
데이터 준비하기
이번에는 MNIST 데이터 세트를 사용합니다. 텐서플로가 설치되어있다는 전제 하에 진행합니다.
import tensorflow as tf
(x_train_all, y_train_all), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
print(x_train_all.shape, y_train_all.shape)
이번에 사용할 데이터는 28X28 크기의 이미지 파일 6만개입니다.
샘플 이미지 확인하기
import matplotlib.pyplot as plt
plt.imshow(x_train_all[0], cmap='gray')
plt.show()
샘플 이미지를 하나 선택하여 matplotlib 라이브러리로 그려봅니다. cmap 매개변수를 gray로 지정하면, 넘파이 배열의 원소 값이 0에 가까울수록 이미지가 검게 그려집니다.
타깃 데이터 확인하기
print(y_train_all[:10])
타깃 데이터의 일부를 출력해서 확인해봅니다. 각 숫자가 의미하는 값은 다음과 같습니다
0. 티셔츠,윗도리
1. 바지
2. 스웨터
3. 드레스
4. 코트
5. 샌들
6. 셔츠
7. 스니커즈
8. 가방
9. 앵클부츠
타깃 분포 확인하기
훈련 데이터 세트를 훈련 세트와 검증 세트로 나누기 전에, 먼저 타깃값의 분포가 어떤지 확인해봅니다.
np.bincount(y_train_all)
확인 결과, 클래스 당 6000개의 데이터가 들어있습니다.
훈련 세트와 검증 세트로 나누기
from sklearn.model_selection import train_test_split
x_train, x_val, y_train, y_val = train_test_split(x_train_all, y_train_all, stratify=y_train_all, test_size=0.2, random_state=42)
print(np.bincount(y_train))
print(np.bincount(y_val))
입력 데이터 정규화하기
x_train = x_train / 255
x_val = x_val / 255위스콘신 유방암 데이터를 사용할 때는 훈련 데이터를 표준화하여 평균 0, 분산을 1에 맞췄습니다. 지금 하는 것은 이전에도 말했지만, 표준화가 아닌 정규화 입니다. 정규화는 데이터의 값을 0~1의 범위로 정규화하는 것입니다.
훈련 세트와 검증 세트의 차원 변경하기
x_train = x_train.reshape(-1, 784)
x_val = x_val.reshape(-1, 784)
print(x_train.shape, x_val.shape)
앞에서 구현한 MultiClassNetwork는 1차원 배열의 샘플을 입력으로 받으므로, 이에 맞게 배열의 차원을 바꿔야 합니다.
타깃 데이터 준비하기
위에서 준비한 MNIST 세트는 10개의 클래스가 있으므로 출력 뉴런의 개수도 10개가 되어야 합니다. 이 출력 뉴런의 값이 타깃값에 대응되어야 하는데, 다중 분류에서의 타깃값은 1 또는 0입니다. 이 출력 뉴런의 값들은 0~9의 값이므로, 10개의 출력 뉴런에 대응되지 않습니다.
원-핫 인코딩
신경망의 출력값과 타깃값을 비교하려면, 타깃값이 출력층의 10개 뉴런에 대응하는 배열이어야 합니다. 그러나 y_train, y_val에 저장된 값을은 배열이 아니라 그냥 0~9의 정수 값입니다. 이에 대한 방법은 출력 뉴런의 수와 같은 크기의 배열을 만들고, 정수 값에 해당하는 인덱스에 해당하는 원소의 값은 1, 나머지는 0으로 할당하는 것입니다. 이런 방법을 원-핫 인코딩이라고 합니다.
원-핫 인코딩을 해야하는 이유는 단순히 위의 이유 뿐이 아닙니다. 경사 하강법을 적용할 때, 가중치의 업데이트는 오차의 크기에 비례합니다.
예를 들어 신경망을 트레이닝 하는 도중에, 타깃 값이 9.앵클 부츠인 샘플을 0.티셔츠/윗도리로 예측했다고 가정해보겠습니다. 이러면 오차는 9가 나올것입니다.
이번엔 타깃 값이 9.앵클 부츠인 또다른 샘플을 사용하여 트레이닝 하는데, 이 샘플을 2. 스웨터로 예측했다고 가정해보겠습니다. 이러면 오차는 7입니다.
위 예시를 보면 앵클 부츠를 티셔츠/윗도리로 예측한것과 스웨터로 예측한것 중 티셔츠/윗도리로 예측한 것이 더 잘못됐다고 보이는데, 실제로 어떤 것이 더 잘못 예측한 것이라고 정할 수 있을까요?
이게 만약 회귀 문제라면 문제가 되지 않습니다. 타깃이 9인 값을 2로 예측한것과 0으로 예측한것 중 더 잘못된것은 0으로 예측한 것입니다. 하지만 분류 문제에서는 어떤 예측이 더 잘못됐는지 정하기가 어렵습니다. 따라서, 더 잘못 예측한 것, 혹은 덜 잘못 예측한 것 없이 그냥 잘못 예측한 것은 모두 똑같이 잘못 예측한 것으로 봐야합니다.

to_catergorical() 함수를 사용하여 원-핫 인코딩 하기
텐서플로는 원-핫 인코딩을 위한 함수를 제공합니다. 먼저, 이 함수가 어떻게 동작하는지 확인해보겠습니다.
tf.keras.utils.to_categorical([0, 1, 3])
to_categorical() 함수는 문자열로 된 레이블은 인코딩하지 못하지만, 우리가 사용한 데이터는 정수 배열이므로 to_categorical()함수를 사용하여 원-핫 인코딩을 할 수 있습니다.
y_train_encoded = tf.keras.utils.to_categorical(y_train)
y_val_encoded = tf.keras.utils.to_categorical(y_val)
print(y_train_encoded.shape, y_val_encoded.shape)
인코딩 된 데이터 중 하나를 출력하여 확인해보겠습니다.
print(y_train[0], y_train_encoded[0])
레이블 6이 6번째 인덱스로 인코딩 되었습니다.
MultiClassNetwork 클래스로 다중 분류 신경망 훈련하기
fc = MultiClassNetwork(units=100, batch_size=256)
fc.fit(x_train, y_train_encoded, x_val=x_val, y_val=y_val_encoded, epochs=40)
코드 실행 중 위와 같이 점이 찍힌다면 훈련이 잘 진행되는 중입니다.
손실 그래프와 훈련 모델 점수 확인하기


이 모델의 정확도는 약 82%입니다. 오차가 약 18%정도나 되기 때문에 실전에 사용하기는 어렵습니다. 제대로 된 모델을 만들기 위해서는 텐서플로같은 전문 딥러닝 패키지를 사용해야 합니다.
텐서플로와 케라스를 사용하여 신경망 만들기
지금까지는 신경망을 직접 구현해봤습니다. 하지만, 직접 구현한 신경망은 실전에 사용할 수 있을 정도의 성능을 기대하기는 어렵습니다. 이제부터는 케라스를 사용하여 신경망을 구현해볼 것입니다.
먼저, 텐서플로와 케라스에 대해 간단히 알아보겠습니다. 다음은 간단한 신경망을 텐서플로를 사용하여 구현한 것입니다.
# 훈련할 가중치 변수 선언
w = tf.Variable(tf.zeros(shape=(1)))
b = tf.Variable(tf.zeros(shape=(1)))
#경사하강법 옵티마이저 설정
optimizer = tf.optimizers.SGD(lr=0.01)
num_epochs = 10
#자동 미분을 위해 연산 과정 기록
for step in range(num_epochs):
with tf.GradientTape() as tape:
z_net = w*x_train + b
z_net = tf.reshape(z_net, [-1])
sqr_errors = tf.square(y_train - z_net)
mean_cost = tf.reduce_mean(sqr_errors)
#손실 함수에 대한 가중치의 그래이디언트 계산
grads = tape.gradient(mean_cose, [w, b])
#옵티마이저에 그래이디언트 반영
optimizer.apply_gradients(zip(grads, [w, b]))
위 신경망을 케라스로 구현하면 다음과 같습니다.
#신경망 모델 만들기
model = tf.keras.model.Squential()
# 완전 연결층 추가
model.add(tf.keras.layers.Dense(1))
# 옵티마이저와 손실 함수 지정
model.compile(optimizer='sgd', loss='mse')
# 훈련하기
model.fit(x_train, y_train, epochs=10)코드의 수가 확 줄어들은 것을 볼 수 있습니다.
케라스를 사용하면, 직관적으로 인공신경망의 층을 설계할 수 있습니다. 예를 들어, 다음과 같은 다중 분류 신경망을 만든다고 가정해봅니다.
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
model.add(Dense(100, activation='sigmoid', input_shape=(784,)))
model.add(Dense(10, activation='softmax'))
model.compile(optimizer='sgd', loss='categorical_crossentropy', metrics=['accuracy'])Sequential 클래스는 말 그대로 '순차적으로 층을 쌓은'신경망 모델이고, Dense 클래시는 모델에 포함된 완전 연결층입니다.
line.4~6은 위 그림을 구현한 코드임을 직관적으로 알 수 있을 것입니다.
line.7에서는 최적화 알고리즘과 손실 함수를 정합니다.
이제, 위 모델을 훈련해보겠습니다.
history = model.fit(x_train, y_train_encoded, epochs=40, validation_data=(x_val, y_val_encoded))
fit() 메서드는 훈련 세트와 검증 세트에서 측정한 값들을 History 클래스 객체에 담아 리턴합니다.
print(history.history.keys())
확인해보니 손실 함수값, 정확도, 검증 세트 손실 함수값, 검증 세트 정확도가 있습니다.
위 값들을 그래프로 확인해보겠습니다.
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.show()
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train_accuracy', 'val_accuracy'])
plt.show()

evaluate()메서드를 사용하면 손실값과 metrics 변수에 추가한 측정 지표를 계산하여 리턴합니다.
loss, accuracy = model.evaluate(x_val, y_val_encoded, verbose=0)
print(accuracy)
우리가 직접 구현한 신경망보다는 더 나은 성능을 보여주긴 하지만, 여전히 실전에는 사용할 수 없을 듯 합니다. 이는 우리가 구현한 모델이 이미지 분류에 적절한 모델이 아니기 때문입니다.
'Study > MachineLearning' 카테고리의 다른 글
| [Do it!]7. 텍스트 분류하기 - 순환 신경망 (0) | 2021.09.09 |
|---|---|
| [Do it!] 6. 이미지 분류하기 - 합성곱 신경망 (0) | 2021.09.07 |
| [Do it!] 4. 2개의 층 연결하기 - 다층 신경망 (0) | 2021.09.06 |
| [Do it!] 3. 훈련 노하우 배우기 (0) | 2021.09.03 |
| [Do it!] 2. 분류하는 뉴런 만들기 - 이진 분류 (0) | 2021.09.03 |