이 포스트는 theconstructsim.com의 Kalman Filters 를 참고하였습니다.
이번 포스트에서 다룰 내용은
- Bayes Filter의 building blocks
- 센서의 노이즈가 예측에 미치는 영향
- 불확실한 상태에서의 로봇의 움직임
- Bayesian filtering의 재귀적인 특성
- 1차원 불연속 베이즈 필터를 구현하는 방법
이번 course에서는 turtlebot simulation package를 사용합니다. 아래 링크를 참조하세요
emanual.robotis.com/docs/en/platform/turtlebot3/simulation/
시뮬레이션 모델은 Waffle 모델을 사용합니다.
waffle 모델을 사용하기 위해서는 환경 변수를 추가하거나, bash shell에 해당 명령을 입력하면 됩니다.
$ export TURTLEBOT3_MODEL=waffle
또는, ~/.bashrc 를 수정하여 맨 밑에 export TURTLEBOT3_MODEL=waffle 를 추가합니다.
사용된 ROS버전은 noetic입니다.
ros noetic을 사용할 경우, 외부의 예시를 다운받을 경우 line1의 주석은 항상 python3로 수정해주세요.
#!/usr/bin/env python >> #!/usr/bin/env python3
이번 포스트 관련 이론은 다음 포스트를 참조하세요
soohwan-justin.tistory.com/2?category=941681
soohwan-justin.tistory.com/8?category=941681
베이즈 필터란 무엇인가?
이 질문에 대해 접근하는 방법 중 하나는 이 용어를 분해해보는 것입니다. 필터(Filter)란, 출력으로써 더 정확한 추정값을 얻기 위해 입력의 노이즈(불확실성)을 제거하는 것입니다. 베이즈(Bayes)란, 베이지안 통계(Bayesian statistics)가 적용됨을 의미합니다. 베이지안 통계에서, 과거의 정보는 불확실성이 있는 상태에서 추정값을 만들기 위해 사용됩니다. 간단히 말해서, 베이즈 필터는 과거의 값을 고려하지 않는 알고리즘에 비해 더 정확한 추정값을 위해 과거의 값을 사용하여 추정하는 알고리즘입니다.
하지만, 칼만 필터 코스에서 베이즈 필터가 왜 나오냐? 하실텐데, 칼만 필터는 베이즈 필터의 한 종류입니다. 따라서, 칼만 필터를 이해하기 위해서는 베이즈 필터를 먼저 알아야 합니다.
2.1. Bayes Filter Localization Example
이제 1차원 로봇 위치 추정에서 베이지안 추론이 어떻게 동작하는지 보겠습니다. 이 예시에서 주어진 환경은 다음과 같습니다. 긴 복도가 있고, 이 복도에서 유일한 특징(features)들은 천장에 달린 조명(sporlights)뿐입니다. 로봇은 빛 감지 센서를 사용하여 이 빛을 감지할 수 있으며, 따라서 로봇이 지금 빛 아래 있는지, 빛이 없는 어두운 복도에 있는지 알 수 있다고 합니다. 하지만, 이 모든 조명빛의 세기는 동일하기 때문에 로봇이 어떤 조명 아래에 있는지는 센서를 통해 알아낼 수 없습니다.
이제 누군가가 복도 어딘가에 로봇을 두고, 우리는 이 로봇이 어디 있는지 모른다고 상상해보겠습니다. 하지만 우리는 로봇이 어디 있는지 찾아야 합니다. 우리는 복도에서 조명이 어디있는지 표시된 지도를 갖고 있고, 로봇의 빛 감지 센서의 출력을 읽을 수 있으며, 로봇에게 전방 또는 후방으로 움직이도록 할 수 있습니다.
가정의 단순화
베이즈 필터를 최대한 간단히 설명하기 위해, 다음과 같이 가정을 단순화 합니다.
- 공간의 불연속화: 우리는 복도에 10개의 다른 grid가 있다고 가정합니다. 로봇은 불연속적인 스텝으로만 움직일 수 있습니다. 즉, 로봇은 이 10개의 grid 중 한 곳에만 위치할 수 있습니다.
- 원형 복도: 복도에 막다른 길이 없다고 가정합니다. 즉, 로봇은 계속해서 전방으로 움직일 수 있습니다. 즉, 만약 로봇이 9번 grid에서 앞으로 움직일 때, 로봇은 0번 grid로 순간이동 한다고 보면 됩니다.

2.2. Bayes Filter Initialization
로봇의 위치에 대한 belief 초기화
처음에는 로봇의 위치에 대한 정보가 하나도 없습니다. 어떤 grid cell에든 위치할 수 있으므로, 가장 좋은 추측은 모든 grid cell에 같은 확률을 할당하는 것입니다. 이 추측은 다음과 같은 그래프로 나타낼 수 있습니다.
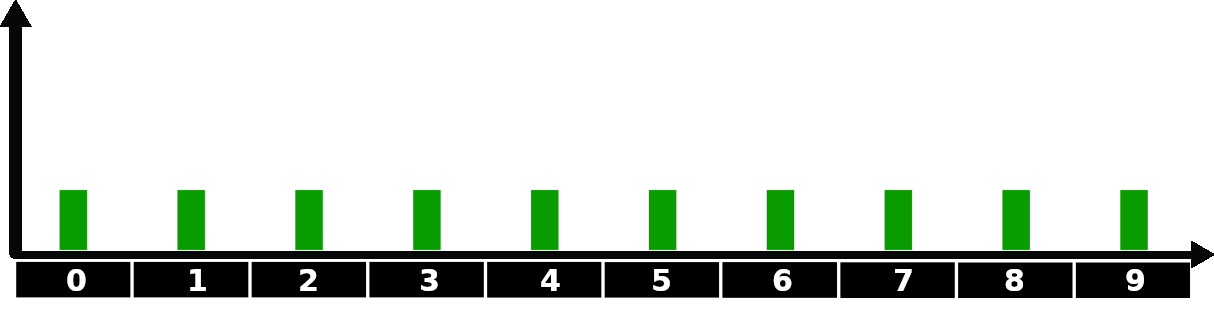
연습 2.1.
다음 명령을 사용하여 예제를 다운받습니다
$ git clone https://bitbucket.org/theconstructcore/kalman_filters_files.git
catkin_make 후, ~/catkin_ws/src/kalman_filters_files/bayes_tutorials/scripts 디렉토리의 bayes_filter.py 파일을 열어봅니다.
### Add initial belief HERE ### << 이렇게 주석처리 된 부분 밑에(아마도 line 19일 것입니다, 초기 belief값을 설정할 수 있습니다.)
베이즈 필터 알고리즘은 환경에 대한 지도가 필요합니다. 이 지도는 로봇이 센서를 통해 감지할 수 있는 특징들로 구성되어있습니다. 우리 예제의 경우, 지도가 어떤 grid cell에 조명이 있고, 없는지를 나타내야 합니다. 이에 대한 설정은
### Add corridor map HERE ### << 이렇게 주석처리 된 부분에서 정의합니다.
ros noetic을 사용할 경우, line1의 주석은 항상 python3로 바꿔주세요.

이제, 다음 명령으로 node를 실행해봅니다.
$ roslaunch bayes_tutorials bayes_filter.launch
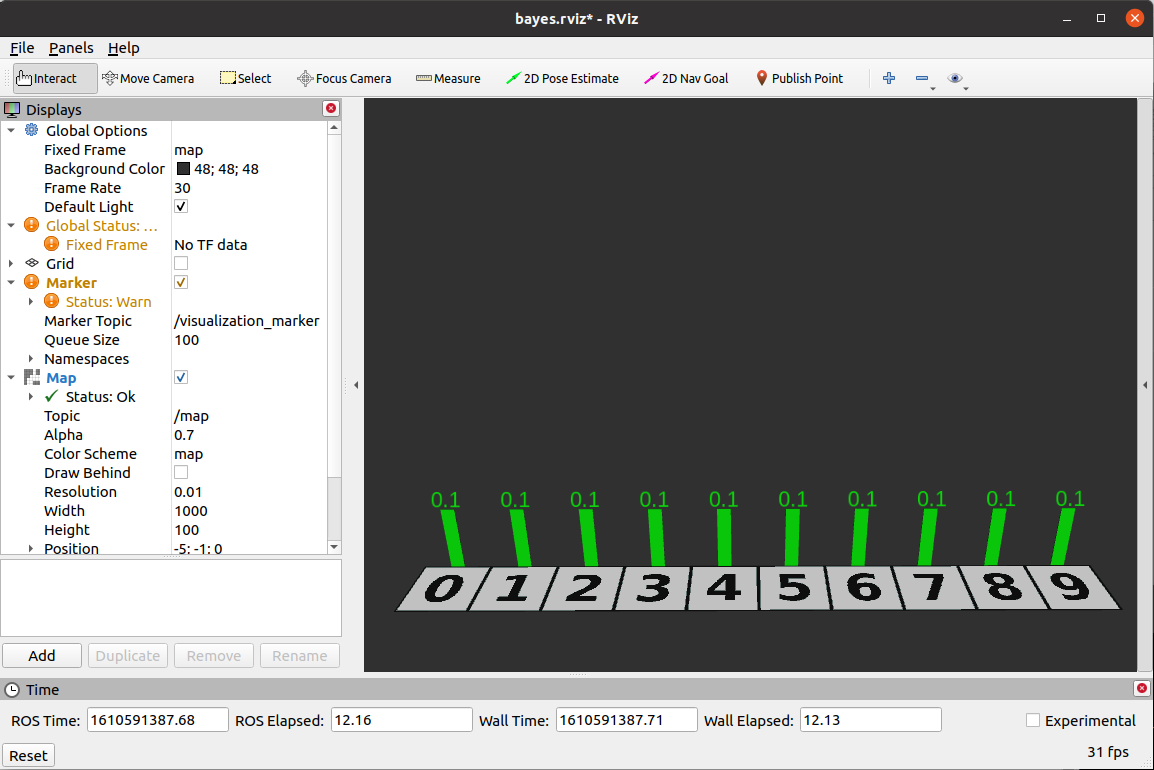
- 연습 2.1. 끝
2.3 Correct Step
correction step은 센서 데이터를 사용하여 센서 데이터와 환경의 지도에 기반하여 추정된 상태를 수정하는 단계입니다. 가끔, 측정(measurement)를 관측(observation)이라고 하기도 하는데, 같은 의미로 보시면 됩니다.
이제, 로봇의 빛 감지 센서를 활용해보겠습니다.
우리는 처음에, 로봇의 위치에 대한 정보가 없으므로 belief를 모두 같게 설정했습니다.
belief = [0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1]
이제 로봇이 빛을 감지하면, 로봇의 위치에 대한 belief가 다음과 같이 바뀝니다.
belief = [0,0.333,0,0.333,0,0,0,0.333,0,0]
이는 지도에 조명이 3개 뿐이고, 우리는 이 조명이 1, 3, 7 grid에 있다는 것을 알고 있습니다.
corridor_map = [0,1,0,1,0,0,0,1,0,0]
따라서 로봇은 1, 3, 7 중 어딘가에 있을 것인데, 아직 이에 대한 정확한 정보는 없으므로 모든 조명에 같은 확률을 할당합니다. 따라서, 다음과 같이 belief가 업데이트 됩니다.
belief = [0,0.333,0,0.333,0,0,0,0.333,0,0]
[0,0.333,0,0.333,0,0,0,0.333,0,0]와 같은 형태의 belief 벡터는 로봇이 있을 확률이 가장 높은 cell을 보여줍니다. 이렇게 업데이트 된 belief를 그래프로 나타내면 다음과 같을 것입니다.

Let's talk about sensor noise
인식을 위해서는, 로봇은 반드시 센서에 의존해야 하지만 센서들은 완벽하지 않기 때문에, 이런 부정확한 데이터를 극복하는 것이 로보틱스에서는 매우 중요한 문제입니다. 센서들은 감지 거리와 해상도가 제한적이며, 노이즈가 있습니다. 불완전함이라는 것은 환경에 대한 영향도 있는데, 예를 들어 진동같은 경우는 잘 측정이 되지 않기도 합니다.
Likelihood
이제, 노이즈의 영향을 받는 빛 감지 센서에 대해 고려해보겠습니다. 로봇이 빛을 감지했다고 했을 때, 복도에서의 위치 변화에 대한 belief에 얼마나 큰 영향을 줄까요? 만약 빛 감지 센서에 노이즈가 있다면, 이전에 계산했던 것처럼 3개의 cell에 1/3의 확률을 똑같이 할당할 수 없을 것입니다. 우리는 센서 측정의 오차에 대한 작은 확률을 계산해야 합니다. 이를 위해서, 우리는 우도(likelihood) 라는 개념을 사용할 것입니다.
우리는 빛이 감지된 위치를 나타내는, 노이즈가 있는 센서 데이터를 받은 후 로봇이 있을 수 있는 위치를 나타내는 벡터를 사용할 것입니다. 간단히 하기 위해, 이 벡터를 단지 두 개의 임의의 값를 가진 벡터로 모델링 합니다. 이 때, 빛이 있을 확률이 낮은 grid cell에는 1을, 확률이 높은 곳에는 3을 할당합니다. 예를 들어 우리의 예제의 경우, 다음과 같이 정의합니다.
likelihood = [1,3,1,3,1,1,1,3,1,1]
이제 Python에서 likelihood를 계산하는 코드를 확인해보겠습니다.
def likelihood(environment_map, z, z_prob):
""" Calculates the likelihood of each grid cell given the sensor's reading """
likelihood = [1] * (len(environment_map))
for index, grid_value in enumerate(environment_map):
if grid_value == z:
likelihood[index] *= z_prob
else:
likelihood[index] *= (1 - z_prob)
return likelihood
이 함수는 환경에 대한 지도 envrionment_map, 센서 데이터 z, 센서 데이터의 정확도 z_prob를 입력으로 받고, likelihood를 리턴합니다. 이 때, 센서 데이터 z는 1 또는 0만 있다고 가정해보겠습니다.
- z = 1 : 빛이 감지된 경우
- z = 0 : 빛이 감지되지 않은 경우
파라미터 z_prob는 센서가 빛을 감지한 grid cells에 할당된 값을 hold합니다. 즉, 센서의 정확도가 높을수록 해당 값이 잘 유지됩니다. 예를 들어, 어떤 grid cell의 likelihood 값이 3이고, 센서의 정확도가 90%이면 최종적으로 해당 값은 2.7이 되는 것입니다.
어두운 영역의 grid cells의 값은 (1 - z_prob)이 곱해지게 됩니다. 이는 센서가 완벽하지 않다는 것을 나타내며, 따라서 센서가 어두운 곳에서도 빛을 감지할 수도 있기 때문에 확률값에 0을 할당하지 않습니다.
위의 함수는 환경 지도의 길이만큼 1로 초기화된 list를 만듭니다. 그 후, 각각의 cell을 업데이트 할 때, 지도와 센서의 데이터가 매치되면(센서의 값과 실제 지도에서 빛의 유무의 값을 비교) z_porb 값을 곱하며 매치되지 않으면 (1 - z_prob)를 곱합니다.
Normalization(정규화)
위에서 정의한 likelihood벡터에서 각 원소의 합이 1이 아니었습니다. 따라서 이 likelihood는 확률 분포가 아닙니다. 사실, likelihood를 다른 용어로 설명하자면, likelihood는 확률이 아니지만, 확률에 비례합니다.
likelihood를 확률 분포 함수로 바꾸기 위해서는, 우리는 각 값의 합이 1이 되도록 고정된 scale factor를 곱하여 스케일을 조절해주면 됩니다. 반면, 변환된 값들의 상대적인 차이는 원래의 값과 동일해야 합니다.
예제에서 likelihood를 정규화하는 것은 그 값들을 바꾸긴 하지만, 여전히 로봇이 빛을 감지할 때는 그렇지 않은 때 보다 3배 큰 값을 갖게됩니다. 우리는 이 scale factor를 normalizer라고 합니다.
likelihood 벡터를 정규화하는 과정은 다음과 같습니다.
- 먼저, 이 공식을 계산합니다 : normalizer = 1 / (likelihood vector의 모든 원소들의 합)
- 그 후, likelihood 벡터의 각각의 값에 normalizer를 곱합니다
예를 들어, 만약 위에서 사용했던 likelihood = [1,3,1,3,1,1,1,3,1,1] 를 정규화한다고 하면, 다음과 같습니다.
모든 원소의 합 : 1+3+1+3+1+1+1+3+1+1 = 16 >> normalizer = 0.0625
따라서, normalized_likelihood = [0.0625,0.1875,0.0625,0.1875,0.0625,0.0625,0.0625,0.1875,0.0625,0.0625]
def normalize(inputList):
""" calculate the normalizer, using: (1 / (sum of all elements in list)) """
normalizer = 1 / float(sum(inputList))
# multiply each item by the normalizer
inputListNormalized = [x * normalizer for x in inputList]
return inputListNormalized
이제는 correct step에 대해 자세히 알아보겠습니다.
correct step은 현재의 belief를 수정하기 위해 센서의 측정값을 사용합니다. 수학적으로 말해서, correct step은 현재의 belief를 likelihood function에 곱하는 것으로 구성됩니다. 즉, 각각의 belief를 각각의 likelihood의 원소에 곱하는 것입니다.
우리는 likelihood가 측정값과 환경의 지도를 비교하여 만들어졌다는 것을 알고있습니다. 추가적으로, correct step은 가능한 값들의 합이 1이 되도록 적절한 확률 분포를 만들기 위해 업데이트된 belief를 정규화 합니다.
def correct_step(likelihood, belief):
output = []
# element-wise multiplication (likelihood * belief)
for i in range(0, len(likelihood)):
output.append(likelihood[i]*belief[i])
return normalize(output)
- 연습 2.2
연습 2.1과 같이 bayes filter node를 실행시키고, 확률 값을 업데이트하는 것을 확인해봅니다.
$ roslaunch bayes_tutorials bayes_filter.launch
$ rosservice call /request_measurement_update "{}"

위 값은 로봇이 위치 0에서 1로 움직였을 때, 업데이트 된 결과를 나타냅니다.
- 연습 2.2 끝
2.4 Predict Step
이제 로봇이 복도를 따라 움직이는 것을 분석해보겠습니다. 이를 위해, 연습 2.2에서 중단했던 위치에서 오른쪽으로 한 칸 움직이도록 명령을 내려봅니다. 이렇게 움직이면 로봇의 위치에 대한 belief가 어떻게 바뀌게 될까요? 오도메트리에 오차가 없기 때문에, 오른쪽으로 한 칸 움직이도록 하면, 모든 belief들이 한 칸씩 오른쪽으로 이동할 것입니다.
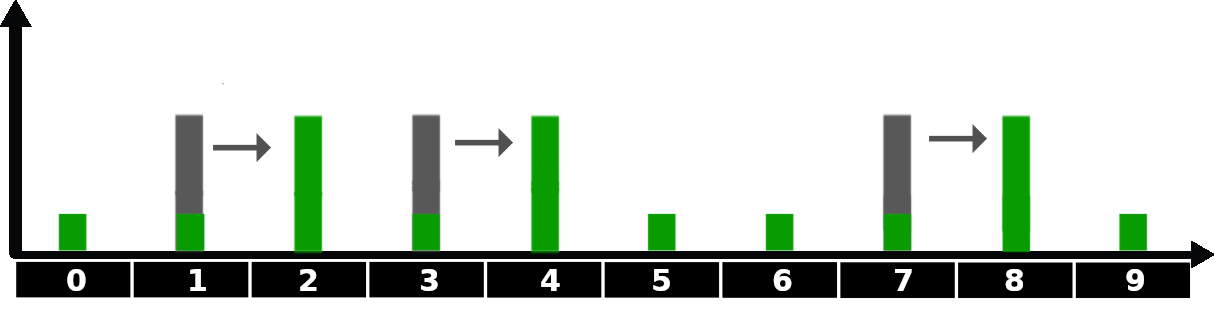
참고로, 위의 그림에서는 아직 센서의 측정은 고려하지 않고, 로봇의 움직임만 고려한 상황입니다. 따라서 확률 분포의 모양은 변하지 않고, 위치만 변했습니다.
Movement noise
이번에는 오도메트리 센서에 노이즈가 있는 경우를 보겠습니다. 센서에 노이즈가 있다면, 로봇의 실제 위치를 완벽하게 report하지 않을 것입니다. 이 경우, 로봇의 실제 움직임은 오도메트리가 나타내는 데이터보다 적게 움직일 수도, 많이 움직일 수도 있습니다. 이런 애매모호함을 그래프로 나타내보면 다음과 같습니다.

위 그림에서 로봇의 초기 위치는 1번 cell입니다. 그 후, 전방으로 3cell 움직이라는 명령을 받습니다. 우리는 로봇이 움직인 후 추정되는 로봇의 위치에서, 예를 들어 오도메트리 데이터와 비교해서 더 짧은 움직임에는 10%, 제대로 된 움직임에는 80%, 더 긴 움직임에는 10%의 확률을 할당할 수 있습니다. 이에 대한 python code는 다음과 같습니다.
belief = [0., 1., 0., 0., 0., 0., 0., 0., 0., 0.]
def noisy_move(belief, distance, p_under, p_correct, p_over):
n = len(belief)
output = [0] * n
for i in range(n):
output[i] = (belief[(i-distance) % n]* p_correct +
belief[(i-distance-1) % n] * p_over +
belief[(i-distance+1) % n] * p_under)
return output
belief = noisy_move(belief, 3, .1, .8, .1)
print(belief)
위 함수를 분석해보겠습니다. 이 함수의 입력은 belief, distance (이동 명령), undershooting(p_under), being spot on(p_correct), overshooting(p_over) 입니다.
함수 내부에서는, 변수 n에 grid map의 길이를 할당하는데, 예제의 경우에는 10입니다. 다음으로, 함수의 출력을 저장할 비어있는 list를 초기화합니다. 마지막으로, 목표 grid cell 결과 주변의 grid cells의 값을 undershooting, overshooting, being spot on 값을 사용하여 업데이트 합니다.
위 함수가 belief를 수정할 때는, belief를 거리에 따라 이동시키는 대신, 로봇이 overshooting하거나 undershooting하는 시나리오를 계산하기 위해 "평평하게" 합니다. 다음 이미지를 보면 알 수 있는데, 로봇이 노이즈가 있는 상태에서 움직이면, 그래프가 약간 부드러워진 상태로 업데이트가 되는 것을 볼 수 있습니다. 이는 노이즈가 있는 움직임에서는 로봇의 위치에 대한 불확실성이 증가한다는 것을 보여줍니다.
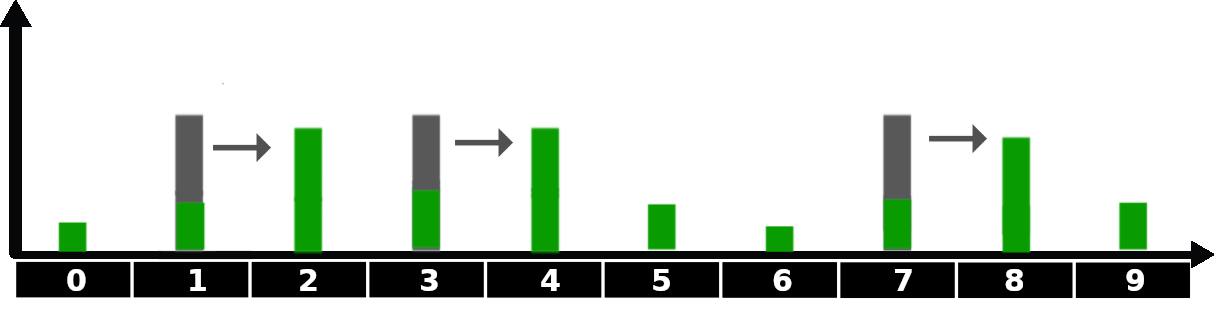
Predict Step as a Sum of two probablity density functions
지금까지는, 로봇의 움직임을 모델링하기 위해서 belief를 같은 거리로 움직이고, 그 움직임의 노이즈의 특징을 나타내는 확률 밀도 함수와 조합한 것을 봤습니다.
두 개의 확률 밀도 함수를 조합하는 수학적 연산을 컨벌루션(convolution)이라고 합니다. 그 결과, 우리는 한 분포의 형태에 어떻게 다른 분포를 "섞을(blends)" 수 있는지를 나타내는 새 확률 분포를 얻을 수 있습니다. 컨벌루션에 대한 자세한 설명은 생략하겠습니다.
컨벌루션을 적용한 predict_step 함수는 다음과 같습니다.
def predict_step(belief, offset, kernel):
"""Applies a convolution by sliding kernel over the belief"""
N = len(belief)
kN = len(kernel)
width = int((kN - 1) / 2)
output = [0] * N
for i in range(N):
for k in range (kN):
index = (i + (width-k) - offset) % N
output[i] += belief[index] * kernel[k]
return output
위 함수는 두 개의 list, belief와 커널을 입력으로 받습니다. 컨볼루션을 하기 이전에, 움직인 거리를 포함하기 위해 offset 값 만큼 커널을 이동합니다. 그 후에, belief에 커널을 적용한 계산을 실행합니다.
probablistic robotics책에 나온 베이즈 필터의 전체적인 알고리즘은 다음과 같습니다.

line 3은 predict step, line 4는 correct step입니다. bel은 belief, u는 제어 명령, z는 센서 값, x는 로봇의 상태입니다. 베이즈 필터는 이렇게 두 과정을 계속 반복하여 점점 정확한 추정값을 갖게 됩니다.
연습 2.3.
다음 명령으로 bayes filter관련 node를 실행하세요.
$ roslaunch bayes_tutorials bayes_filter.launch
$ roslaunch bayes_tutorials simulated_robot.launch
그 후, 다음 명령을 보내면 한 칸씩 이동하며 데이터를 업데이트 하는 것을 볼 수 있습니다. data값을 바꾸면 해당 값 만큼 이동합니다.
$ rostopic pub -1 /movement_cmd std_msgs/Int32 "data: 1"

- 연습 2.3. 끝
'Study > [ROS] KalmanFilter' 카테고리의 다른 글
| Kalman Filter(4. Particle Filter) (0) | 2021.09.02 |
|---|---|
| Kalman Filters(3. Extended Kalman Filter and Unscented Kalman Filter) (0) | 2021.08.30 |
| Kalman Filters (2. Kalman Filter) (0) | 2021.01.20 |