이 포스트는 theconstructsim.com의 Kalman Filters 를 참고하였습니다.
이번 포스트에서 다룰 내용은
- 비선형 함수를 다루기 위한 각각의 필터에 대한 이해
- 비선형 함수를 다루기 위해 칼만 필터가 어떻게 수정되었는가
- robot_localization 패키지를 사용하여 EKF 및 UKF 알고리즘 테스트
이번 course에서는 turtlebot simulation package를 사용합니다. 아래 링크를 참조하세요
emanual.robotis.com/docs/en/platform/turtlebot3/simulation/
시뮬레이션 모델은 Waffle 모델을 사용합니다.
waffle 모델을 사용하기 위해서는 환경 변수를 추가하거나, bash shell에 해당 명령을 입력하면 됩니다.
$ export TURTLEBOT3_MODEL=waffle
또는, ~/.bashrc 를 수정하여 맨 밑에 export TURTLEBOT3_MODEL=waffle 를 추가합니다.
사용된 ROS버전은 noetic입니다.
ros noetic을 사용할 경우, 외부의 예시를 다운받을 경우 line1의 주석은 항상 python3로 수정해주세요.
#!/usr/bin/env python >> #!/usr/bin/env python3
이번 포스트 관련 이론은 다음 포스트를 참조하세요
3.3 The Extended Kalman Filter (tistory.com)
칼만 필터는 많은 응용분야에 적용될 수 있지만, 치명적인 한계가 있습니다. 바로, 오차가 Gaussian임을 가정하며, 이는 linear state transition의 경우만 적용 가능합니다.
하지만 실제 시스템은 선형적이지 않으며, 노이즈 또한 Gaussian이 아닙니다. 예를 들어, 로봇이 원 궤적을 따라가며 비선형적인 움직임을 한다고 가정해보겠습니다.
연속적인 비선형 함수의 가장 큰 단점은 필요한 계산이 너무 많다는 것입니다. 추정 알고리즘은 실제 적용될 때 매우 빠른 속도로 반복되어야하기 때문에 이는 큰 문제입니다.
Handling Nonlinearity
특별히 비선형 문제를 다루기 위해 칼만 필터로부터 생긴 알고리즘은 굉장히 많습니다. 이번 챕터에서는 그 알고리즘 중 확장 칼만 필터(Extended Kalman Filter, EKF)와 무향 칼만 필터(Unscented Kalman Filter, UKF)를 알아볼 것입니다. 이 알고리즘들은 여러 종류의 비선형 근사 방법들을 적용하여 연속적이며 비선형적이고, non-Gaussian인 경우에 대한 계산 복잡도를 다룹니다.
1. Extended Kalman Filter
EKF는 비선형 시스템의 state transition과 measurement functions를 선형근사하여 다룹니다. 기본적으로, 이는 우리가 비선형 함수의 매우 작은 부분을 매우 짧은 직선들로 나눌 수 있다는 것을 가정합니다. 그리고, 이를 필터의 predict step과 correct step 의 선형화(linearize) 계산에 활용합니다.
비선형 함수를 선형화 하기 위해, EKF는 1차 테일러 급수 전개를 사용합니다. 이는 선형화의Jacobian matrix method라고도 합니다. 자코비안 행렬(Jacobian matrix)는 함수의 요소들에 대해 그 함수를 1차 편미분한 행렬입니다. 이는 비선형 함수의 출력이 각각의 입력에 대해 원래의 비선형 관계가 아닌, 선형적인 방법으로 어떻게 변하는지를 알려줍니다.
수학적으로 표기하자면, 함수 $\bf f$의 자코비안 행렬은 $m \times n$ 행렬로 정의되며, $\bf J$로 나타내고, 이 행렬의 $(i, j)$요소는 $\bf{J}_{\it ij} = \it \frac{\partial f_i}{\partial x_j}$ 와 같이 나타내며, 이 식을 자세히 나타내면 다음과 같습니다.
$\bf J =
\begin{bmatrix}
\frac{\partial\bf f}{\partial \mathcal x_1} & \dots &
\frac{\partial\bf f}{\partial \mathcal x_n}
\end{bmatrix} =
\begin{bmatrix}
\frac{\partial \mathcal f_1}{\partial \mathcal x_1} & \dots &
\frac{\partial f_1}{\partial \mathcal x_n}\\
\vdots & \ddots & \vdots \\
\frac{\partial \mathcal f_m}{\partial \mathcal x_1} & \dots &
\frac{\partial f_m}{\partial \mathcal x_n}
\end{bmatrix}$
Jacobian matrix 에 대해 더 자세한 내용은 Khan Academy Lesson on Jacobians 를 참조하세요
2. Example : Jacobian Matrix for an Unicycle motion model
다음과 같이 외바퀴 모델(unicycle model) 로봇의 state transition function을 정의해보겠습니다. 로봇의 균형을 잡는 문제는 무시하고, unicycle state에는 두 개의 input만 있다고 가정합니다.
- 바퀴의 회전 속도는 $v_t$입니다
- z축을 기준으로 바퀴의 방향은 $\omega _t$입니다.
시간 t에서의 control input $u_t$를 벡터 형태로 나타내면 다음과 같습니다.
$\bf u_t = \mathcal{\left[ v_t, \omega _t \right]}$
새로운 pose $\bf x$를 나타내는 가장 간단한 형태의 output 벡터는 다음과 같습니다.
$\bf x_t = \mathcal{\left[ x_t, y _t, \theta _t \right]}$
여기서 $x_t, y_t$는 2차원 평면에서의 x, y좌표이고, $\theta _t$는 방향을 나타냅니다.
이제 입력과 출력의 관계를 나타내주는 상태 과도 함수(state transistion functions) $\bf f$를 정의할 것입니다. unicycle transition model의 비선형 함수들은 다음과 같습니다.
$x_{t+1} = x_t + v_t\cos\theta$
$y_{t+1} = y_t + v_t\sin\theta $
$\theta_{t+1} = \theta_t + \omega$
우리는 위의 state transition functions를 행렬 형태로 다시 쓸수 있습니다. $\bar{\bf x}$는 업데이트된 상태, $\bf F$는 state transition matrix, $\bf x$를 이전의 상태라고 하면, $\bf B$는 control matrix이고 $\bf u$는 control vector이고, 다음과 같이 나타낼 수 있습니다
$\bar{\bf x} = \bf {Fx + Bu}$
이 식을 풀어서 쓰면 다음과 같습니다.
$\begin{bmatrix}x_{t+1} \\ y_{t+1} \\ \theta_{t+1}\end{bmatrix} =
\begin{bmatrix}1 & 0 & 1\\
0 & 1 & 0\\
0& 0& 1
\end{bmatrix}
\begin{bmatrix}x_t \\ y_t \\ \theta_t\\
\end{bmatrix}
+
\begin{bmatrix}\cos(\theta) & 0\\
\sin(\theta) & 0\\
0& 1
\end{bmatrix}
\begin{bmatrix}v_t \\ \omega_t \\
\end{bmatrix}$
따라서,
$\bf {F} = \begin{bmatrix}1 & 0 & 1\\
0 & 1 & 0\\
0& 0& 1
\end{bmatrix}$
$\bf B = \begin{bmatrix}\cos(\theta) & 0\\
\sin(\theta) & 0\\
0& 1
\end{bmatrix}$
입니다.
참고로, probabilistic robotics에서는 위 식에서 노이즈 $\varepsilon_t$ 까지 고려하여 다음과 같이 나타냅니다.
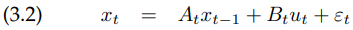
이제 이전에 정의했듯이, 자코비안 행렬을 얻기 위해서, 우리는 state transition functions $\bf f$를 상태에 관해 다음과 같이 편미분 해야합니다.
\begin{bmatrix}
\frac{dx}{dx} & \frac{dx}{dy} & \frac{dx}{d\theta}
\\\frac{dy}{dx} & \frac{dy}{dy} & \frac{dy}{d\theta}\\
\frac{d\theta}{dx} & \frac{d\theta}{dy} & \frac{d\theta}{d\theta}
\end{bmatrix}
$\frac{d\sin(x)}{dx} = \cos(x)$, $\frac{d\cos(x)}{dx} = -\sin(x)$이므로, 위 식을 계산하여 자코비안 행렬 $\bf G_{\mathcal t}$를 계산하면 다음과 같습니다.
$\bf G_{\mathcal{t}} = \begin{bmatrix}
1 & 0 & -v\sin(\theta) \\
0 & 1 & v\cos(\theta) \\
0& 0& 1\end{bmatrix}$
3. A Jacobian Matrix for the measurement model?
우리가 비선형 측정을 다루어야만 하는 특정 상황들이 있습니다. 예를 들면, 로보틱스에서 레이더 센서는 가끔씩 극좌표계로 측정한 데이터를 제공합니다. 이 데이터는 estimation filter에 입력으로 들어가기 전에 반드시 직교좌표계 데이터로 변환되어야 합니다. 이 변환은 비선형 함수인 삼각함수, 즉 사인함수, 코사인함수를 사용하기 때문에 우리는 비선형 측정 모델을 사용하는 상황에 직면하게 됩니다.
다행이도, 우리는 이런 상황을 Jacobian matrix를 사용하여 다룰 수 있습니다. 즉, 이전에는 로봇이 비선형적인 움직임을 선형화 하는것이라면, 이번에는 센서의 비선형적인 데이터를 선형화 하는것입니다.
수학적으로 정의하자면, 현재 상태 변수 $\bf x$에서의 측정값(measurements) $z_t$에 관한 측정 함수(measurement function) $\bf h$가 주어졌을 때, 자코비안 행렬 $\bf H_{\mathcal{t}} = \frac{\mathcal{d}\bf h}{\mathcal{d} \bf x}$ 입니다.
그러므로 EKF는 state transition model을 위한 $\bf G$와 measurement model을 위한 $\bf H$ 이렇게 두 개의 다른 자코비안 행렬을 필요로 한다는 것을 기억하세요
4. EKF Predict Step
자코비안 행렬 $\bf G$가 정의됐다고 가정하면, 예측 단계(predict step)에서 첫 번째 단계는 $\bf G$를 사용하여 가장 최근의 상태 추정값으로 업데이트하는 것입니다.
Mean Update
EKF도 KF와 같은 방식으로 평균을 업데이트 하는데, 그냥 단지 아래의 식에서 non-linear state transition model을 적용합니다.
$\bar{\bf x} = \bf Fx + Bu$
여기서 $\bar{\bf x}$는 업데이트된 상태, $\bf F$는 state transition matrix, $\bf x$, $\bf B$는 control matrix, $\bf u$는 control vector입니다.
Covariance update
우리는 $\bf F$를 $\bf G$로 치환하여 공분산 행렬 $\overline{\bf P}$를 업데이트할 수 있습니다.
즉, 칼만 필터에서의 $\overline{\bf P} = \bf{FPF}^{\tt T} + Q$에서, 다음과 같이 바뀌게 됩니다.
$\overline{\bf P} = \bf{GPG}^{\tt T} + Q$
그리고, 이 결과는 EKF의 predict step에 관련된 것입니다. predict step은 control에 의한 추정, correct step은 measurement에 의한 추정이라고 보시면 됩니다.
5. EKF Correct Step
먼저, residual을 계산합니다.
$\bf y = z-H\overline{x}$
여기서 $\bf \overline{x}$는 predict step에서의 평균입니다.
다음으로, innovation(또는 residual) 행렬 $\bf S$를 계산합니다.
$\bf S = \bf{H\overline{P}H}^{\tt T} + R$
다음으로, 칼만 이득 $\bf K$를 계산합니다.
$\bf K = \overline{P}H^{\tt T}S^{-1}$
여기서 $\bf \overline{P}$는 predict_step으로부터 계산한 공분산 행렬입니다.
Mean update
$\bf x = \overline{x} + Ky$
이전과 같이, 업데이트 된 평균을 구한 이후에는 업데이트 된 공분산 행렬을 구합니다.
Covariance update
$\bf P = (I-KH)\overline{P}$
여기서 $\bf P$는 새로운 공분산 행렬, $I$는 identity matrix, $\bf K$는 칼만 이득 행렬, $\bf H$는 측정 모델, $\bf \overline{P}$는 predict_step으로부터의 공분산 행렬입니다.
만약 모델을 선형화 해야하는 경우에는 칼만 필터의 $\bf H$를 자코비안 행렬 $\bf H$로 바꿔야 합니다. 이러 ㄴ경우에는 correct_step에서 가장 먼저 해야할 것은 이전 상태의 추정값을 사용하여 자코비안 행렬 $\bf H_{\mathcal{t}}$를 업데이트 하는 것입니다. 이는 반드시 correct_step이 호출될 때마다 이루어져야 합니다.
6. EKF localization demo
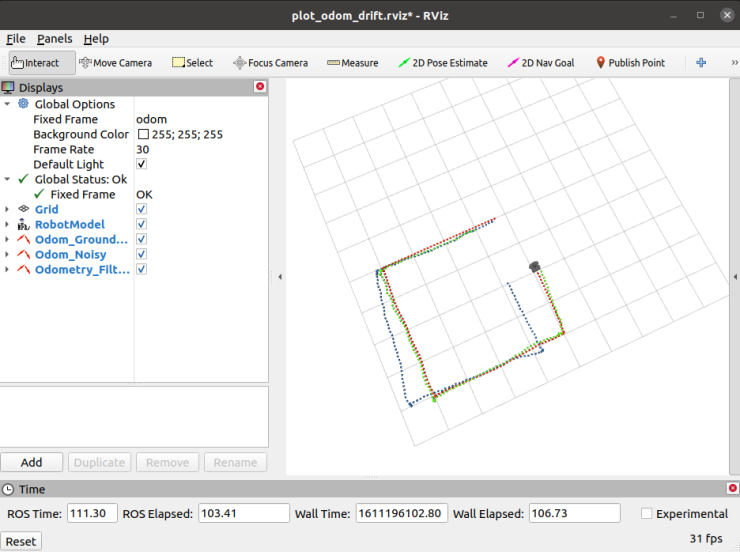
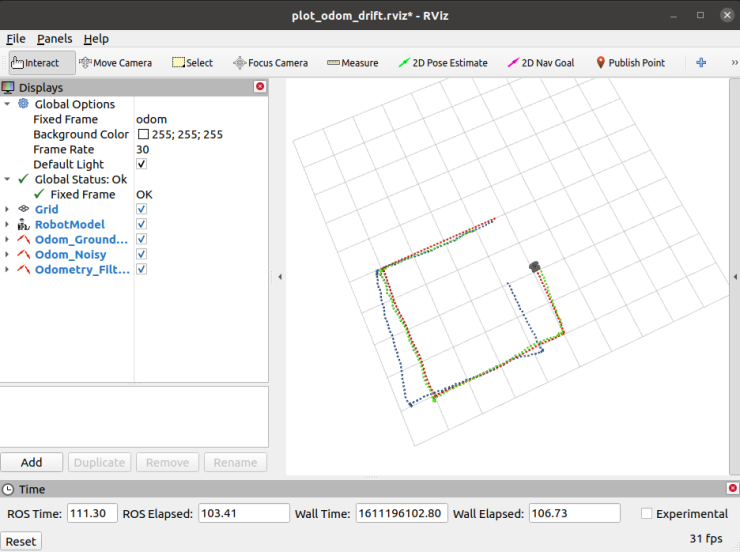
일단 먼저 EKF 적용 결과를 보면, 위와 같습니다. 로봇은 완벽한 정사각형으로 계속 움직이고 있으며, 해당 경로는 빨간 점으로 표시되었습니다. 우리는 파란색 점선도 볼 수 있는데, 이는 빨간색 점선 만큼 완벽하지 않으며, 이 값은 노이즈가 섞인 오도메트리 데이터입니다. 초록색 점선은 IMU데이터와 오도메트리 데이터를 사용하여 필터링한 후 나타낸 데이터입니다.
위의 결과에서 알 수 있듯이, 노이즈로 인해 경로들이 실제 로봇이 움직인 경로와 다르다는것을 알 수 있습니다. 하지만, EKF를 통해 단일 센서만 사용하는 것 보다 훨씬 정확한 위치 정보를 얻을 수 있습니다.
7. The ekf_localization ROS node explained
robot_localization ROS 패키지는 EKF 또는 UKF에 기반한 3D 공간에서 비선형적으로 움직이는 로봇의 state estimation을 제공합니다. 이번에는 EKF의 코드를 한번 살펴보겠습니다. ekf.cpp 에서 코드 전체를 확인할 수 있습니다.
Correct step
line 55에서 correct() 함수를 찾을 수 있습니다. 먼저, 다음 부분을 살펴보겠습니다.
1. measurement의 어떤 state variables가 필터를 통과할지 결정합니다. 가끔씩, 센서는 NaN(not a number) 또는 무한대의 측정값 InF를 리턴합니다. NaN은 센서로 들어온 데이터가 없는 것입니다. 이 함수는 이런 값들을 감지하고, 유용한 정보들만 필터에 사용되도록 합니다.

2. 위의 filter step을 통과한 state variables에 따라 sub-matrices를 초기화합니다.

3. measurement matrix $\bf z$와 measurement covariance matrix $\bf R$을 채웁니다. 여기서는 covariance matrix를 나타내기 위해 line 97에서 $\bf P$ 대신 $\bf R$이 쓰였습니다.

4. state-to-measurement matrix $\bf H$를 채웁니다.

5. 칼만 이득 $\bf K = \overline{P}H^{\tt T}S^{-1}$을 계산합니다.

6. innovation $\bf y = z-H\overline{x}$를 계산합니다.

7. Mahalanobis distance를 사용하여 어떤 입력을 사용하고 무시할지 결정하기 위해 outliers를 감지합니다. 그리고 새로운 추정된 상태 평균(estimated state mean) $\bf x = \overline{x}+Ky$와 새로운 공분산 추정 $\bf P = (I-KH)\overline{P}$를 계산합니다.

Predict Step
line 210의 predict()함수 부분부터 시작합니다.
1. 자주 사용되는 변수와 함수를 선언합니다.

2. 상태 과도 함수(state transition finction, 전달 함수 transfer function 이라고도 합니다) $\bf F$를 omnidirectional motion model(전 방향 운동 모델)에 기반해서 계산합니다.

3. 자코비안 $\bf G$를 계산합니다.


4. 노이즈 공분산 $\bf Q$를 계산합니다.

5. 단일 입력이 사용될 경우, control terms $\bf Bu$를 적용합니다

6. 새로운 상태 평균 $\bf \overline{x} = Fx + Bu$를 계산합니다.
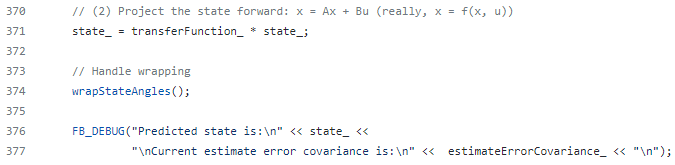
7. 새로운 상태 공분산 $\bf \overline{P} = GPG^{\tt T} + Q$를 계산합니다.
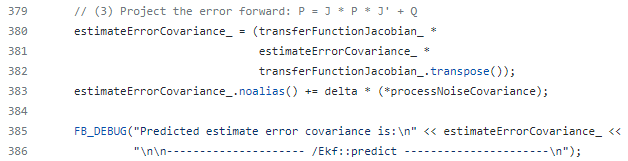
8. UKF Predict Step
가끔씩은 비선형 문제를 위한 EKF도 동작하지 않는 경우가 있습니다. 이는 모든 비선형 문제들이 다 같지는 않기 때문입니다. 어떤 함수들은 일부분만 비선형인 경우도 있고, 그냥 전부 다 비선형인 경우도 있습니다. EKF는 비선형 함수에서 아주 작은 구간을 선형으로 근사하여 추정하는 원리를 사용합니다. 그리고 EKF는 직선을 곡선에다가 맞추려고 하기 때문에, 추정값은 반드시 어느정도 오차를 가질 수 밖에 없습니다. 약간만 비선형인 모델에서는 EKF가 어느정도 오차가 있음에도 불구하고 "진짜 상태(true state)" 값을 가질 수도 있습니다. 하지만 만약 선형인 부분이 거의 없는 문제라면, 필터가 반복될 때마다 오차가 존재하게 될 것이고, 이로 인해 나쁜 추정값을 갖게 될 것입니다. 그 결과, 추정값은 시간에 따라 현저하게 값이 나빠지게 될 것입니다. 단지 몇 번의 반복 이후에도, EKF는 발산하거나 실제 값과 별로 대응되지 않는 결과를 보이기 시작할 것입니다.
Uscented Kalman Filter(UKF)는 EKF가 하는 것 처럼 단순히 선형화하는 것 보다는 더 나은 방법으로 비선형 시스템을 다루기 위해 만들어졌습니다. UKF의 주요 아이디어는 현재 상태 주변에서 몇 개의 샘플링 포인트를 만들어 내고, 이를 사용하여 시스템 방정식(system equations)을 근사화 하고, 그 상태를 비선형 함수를 통해 사영(project)하며, 새로운 상태와 공분산을 얻기 위해 변환된 샘플링 포인트들의 gaussian을 계산합니다.
9. UKF Predict Step
predict_step에서 칼만 필터는 일부 이전 상태의 값과 state transition function을 사용하여 상태에 대한 예측값을 만들었습니다.
UFK는 몇 개의 샘플링 포인트(sigma point라고 합니다)를 주된 양상(main aspect)으로써 사용하여 비선형 transition function을 다룹니다. sigma point는 기본적인 비선형 함수를 몇 개의 데이터 값으로 인코딩하기 위해 covariance에 기반한 가장 최근의 state estimate mean 주변에서 명시적으로 선택됩니다. 그 후, 이 sigma points는 비선형 transition equations를 통해 변환되고, 새로운 predict_step state estimate를 얻기 위해 최종적으로 새로운 가우스 분포로 디코딩됩니다. 몇 개의 sample points를 취함으로써, 비선형 함수 근사는 하나의 점, 평균에서의 값 만을 사용하여 선형화를 하는 EKF 근사와 비교하여 더 정확해지게 됩니다.
UKF의 predict_step function이 어떻게 적용되었는가 하는가에 대한 자세한 내용은 다음과 같습니다.
1. 가장 최근의 평균과 분산으로부터 sigma points를 계산합니다 : UFK의 첫 번째 step은 가장 최근의 추정으로부터 sigma points와 이에 대응되는 가중치를 계산하는 것입니다. sigma points와 가중치를 선택하는 방법은 링크를 참조하세요
보통, sigma points와 가중치들은 다음과 같이 행렬에 저장됩니다.
$weights = \begin{bmatrix}w_0 & w_1 & \dots & w_n\end{bmatrix}$
$sigmas =
\begin{bmatrix}
\mathcal{X}_{0, 0} & \mathcal{X}_{0, 1} & \dots & \mathcal{X}_{0, n} \\
\mathcal{X}_{1, 0} & \mathcal{X}_{1, 1} & \dots & \mathcal{X}_{1, n} \\
\vdots & \vdots & \ddots & \vdots \\
\mathcal{X}_{n, 0} & \mathcal{X}_{n, 1} & \dots & \mathcal{X}_{n, n} \\
\end{bmatrix}$
2. 비선형 함수를 통해 모든 sigma points를 하나씩 통과시킵니다 : sigma points는 비선형 state transition equations를 통해 수학적으로 새로운 state estimate를 예측하기 위해 사용됩니다.
3. 새로운 transformed points로부터 Gaussian평균과 분산을 계산합니다 : 새로운 state prediction은 모든 points가 비선형 함수를 통과한 후의 sigma points로부터의 새로운 Gaussian distribution을 reconstructing하는것에 의해 예측됩니다.
4. 새로운 평균과 분산을 리턴합니다.
10. UKF Correct Step
correct_step은 센서로부터의 데이터를 받아 실제의 평균, 분산과 예측된 평균분산의 차이를 계산합니다. UKF의 correct_step은 다음과 같이 구성됩니다.
1. state space로부터 state prediction을 measurement state space로 가져옵니다 : state space에서 생성된 sigma points를 measurement function $h(x)$를 사용하여 measurement space(센서 데이터가 제공되는 공간)으로 변환합니다.
$\mathcal{Z} = h(\mathcal{X})$
여기서 $\mathcal{Z}$ 는 measurement space로 변환된 sigma points를 의미하고, $h(x)$는 sigma points를 measurement space로 맵핑하는 함수, $\mathcal{X}$는 sigma points matrix 입니다.
※ state space를 measurement space로 변환하여 모든 값들이 같은 단위를 갖도록 하는 함수 $h()$가 필요합니다.
2. transformed points의 집합으로부터 새로운 measurement mean을 계산합니다 : 각각의 sigma point는 그에 관련된 가중치를 갖습니다. 새로운 measurement mean estimate는 가중치가 적용된 모든 sigma points를 더함으로 인해 만들어집니다.
3. 새로운covariance matrix를 계산합니다 : 우리는 predicted measurement covariance matrix $\bf P_z$를 계산하기 위해 sigma point measurement와 predicted measurements를 사용합니다.(밑첨자 $\bf z$는 measurement sigma points의 평균과 분산을 나타냅니다)
4. cross correlation matrix를 계산합니다 : 우리는 state space의 sigma points와 measurement space의 sigma points사이의 measurement cross-covariance matrix $\bf P_{\mathcal{xz}}$를 계산하기 위해 sigma point measurements와 predicted measurement를 사용합니다. 이를 위해 상태 x와 x-space의 sigma points의 차이점 뿐 아니라 measurement z와 z-space의 sigma points사이의 차이점도 고려해야 합니다.
5. Kalman 이득을 결정합니다 : correlation matrix $\bf P_{\mathcal{xz}}$, predicted covariance matrix $\bf P_z$로부터 칼만 이득을 계산합니다.
$\bf K = P_{\mathcal{xz}P^{-1}_{z}}$
6. 최종적으로, 새로운 평균을 계산합니다 : residual $\bf y$와 칼만 이득 $\bf K$를 사용합니다
$\bf x = \bar{x} + Ky$
7. 새로운 covariance를 얻습니다. :
$\bf P = \bar{P} - KP_zK^{\tt T}$
10. Configuring the robot_localization package
다음 예제에서는, robot_localization 패키지를 사용하여 UKF를 실행하기 위해 설정하는 방법을 알아볼 것입니다. IMU데이터와 오도메트리 데이터를 받아 로봇의 위치를 추정해볼 것입니다.
다음과 같이 ukf_filtering이라고 하는 패키지를 만듭니다.
| $ cd ~/catkin_ws/src $ catkin_create_pkg ukf_filtering $ cd ukf_filtering $ mkdir launch $ mkdir config |
robot_localization 패키지는 launch 파일로 설정합니다. 필요하다면 여러개의 ukf node를 실행할 수 있지만, 이번에는 하나의 node만 실행할 것입니다.
/launch 디렉토리에서 ukf_filtering.launch 파일을 만들고, 다음과 같이 작성해봅니다.
<launch>
<!-- Run the UKF Localization node -->
<node pkg="robot_localization" type="ukf_localization_node" name="ukf_localization_node" clear_params="true">
<rosparam command="load" file="$(find ukf_filtering)/config/ukf_localization.yaml"/>
</node>
</launch>
위 파일은 ukf_localization.yaml 설정 파일을 사용하여 robot_localization 패키지로부터 ukf_localization_node ROS 프로그램을 실행합니다.
이제, /config 디렉토리에서 ukf_localization.yaml파일을 만들고, 다음과 같이 입력합니다
#Configuation for robot odometry EKF
frequency: 50
two_d_mode: true
publish_tf: false
# Complete the frames section
odom_frame: odom
base_link_frame: base_link
world_frame: odom
# map_frame:
# Complete the odom0 configuration
odom0: odom_noisy
odom0_config: [false, false, false,
false, false, false,
true, true, false,
false, false, true,
false, false, false]
odom0_differential: false
# Complete the imu0 configuration
imu0: imu
imu0_config: [false, false, false,
false, false, true,
false, false, false,
false, false, true,
true, false, false]
imu0_differential: false
# The process noise covariance matrix can be difficult to tune, and can vary for each application, so it
# is exposed as a configuration parameter. The values are ordered as x, y, z, roll, pitch, yaw, vx, vy, vz,
# vroll, vpitch, vyaw, ax, ay, az. Defaults to the matrix below if unspecified.
process_noise_covariance: [0.05, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0.05, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0.06, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0.03, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0.03, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0.06, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0.025, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0.025, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0.04, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0.01, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.01, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.02, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.01, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.01, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.015]
# This represents the initial value for the state estimate error covariance matrix. Setting a diagonal value (a
# variance) to a large value will result in early measurements for that variable being accepted quickly. Users should
# take care not to use large values for variables that will not be measured directly. The values are ordered as x, y,
# z, roll, pitch, yaw, vx, vy, vz, vroll, vpitch, vyaw, ax, ay, az. Defaults to the matrix below if unspecified. -->
initial_estimate_covariance: [1e-2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 1e-2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1e-2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 1e-2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1e-2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 1e-2, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1e-2, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 1e-2, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 1e-2, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 1e-2, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1e-2, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1e-2, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1e-2, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1e-2, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1e-2]
이제 위 코드를 분석해보겠습니다.
frequency: 50
two_d_mode: true
publish_tf: false
첫 번째 파라미터는 frequency를 Hz단위로 설정하며, 이 주기로 필터의 위치 추정 output을 내보냅니다.
two_d_mode는 로봇이 2D환경에서 동작할 경우 true로 설정합니다.
이 node는 world_frame 파라미터에 정의된 좌표 프레임에 따라 odom -> base_link 좌표변환 또는 map -> odom 좌표변환을 publish할 수 있습니다. 만약 publish_tf 파라미터를 true로 설정한다면, 같은 좌표변환을 broadcasting해서 충돌하게되는 다른 node가 없는지 확인해야 합니다.
The reference frames
# Complete the frames section
odom_frame: odom
base_link_frame: base_link
world_frame: odom
# map_frame:
- base_link_frame : 이 프레임은 로봇 그 자체이며, 어떤 센서든 이 프레임을 기준으로 할 수 있습니다. 이는 보통 로봇의 회전 중심에 놓입니다.
- odom_frame : 오도메트리 데이터를 report하기 위해 사용되는 프레임 입니다.
- map_frame : 예를 들면 AMCL같이 로봇의 글로벌 좌표를 아는 시스템으로부터 해당 값을 report하기 위해 쓰이는 프레임 이름입니다. 만약 local sensor만 사용한다면 생략합니다.
- world_frame : odom_frame또는 map_frame 중에서, world에서의 로봇의 절대 좌표를 얻기 위해 사용될 reference frame을 정합니다.
Adding sensors to fuse
다음 메시지 포맷으로 발행되는 모든 메시지들은 robot_localization 패키지에서 입력으로 사용될 수 있습니다.
- nav_msgs/Odometry
- sensor_msgs/Imu
- geometry_msgs/PoseWithCovarianceStamped
- geometry_msgs/TwistWithCovarianceStamped
또한, 우리는 센서의 종류에 상관 없이 여러개의 센서를 사용할 수 있습니다. 예를 들어, 우리는 2개의 sources, 예를 들어 wheel odometry와 visual odometry를 사용할 수도 있고, 두 개 이상의 IMU센서의 데이터를 사용할 수도 있습니다.
이번 예제에서는 IMU와 wheel odometry데이터를 사용할 것입니다. robot_localization 센서들은 메시지 타입(odom, imu, twist, pose)의 접두사와 0부터 순차적으로 증가하는 숫자로 표시됩니다. 각각의 값은 센서가 publish하는 topic의 이름입니다.
위에서 작성한 코드에서는 /odom_noisy topic과 /noisy_imu topic을 받아서 필터링합니다.
odom0: odom_noisy
imu0: imu
Configure each sensor's variables matrix
파라미터 imu0_config와 odom_config는 사용자가 현재 상태를 추정하기 위해 어떤 센서들이 사용될지를 결정하게 해줍니다. 특정 변수를 활성화 또는 비활성화를 하고 나면, 각 요소의 값이 true 또는 false값을 갖는 3x5 크기의 행렬을 반드시 정의해야 합니다.
wheel odometry sensor matrix를 설정하려면 어떻게 해야할까요?
wheel encoders는 일반적으로 absolute pose와 즉각적인 속도 정보를 제공합니다. robot_localization 문서에서는 다음과 같이 설명되어있습니다. "만약 오도메트리가 위치(X, Y, Z 정보)와 선 속도 정보 모두를 제공한다면, 선 속도 값을 조합하세요". 이 원칙은 로봇의 방향(orientation)과 각속도에 대해서도 적용됩니다. 즉, 우리는 absolute yaw가 아니라 wheel encoder로부터 yaw velocity를 사용해야 한다는 것입니다. 오도메트리 데이터로부터 absolute pose variables는 사용되면 안되는데, 대부분의 시간에서 해당 변수들의 값은 적분으로부터 구해지는데, 따라서 시간이 지남에 따라 이 추정값의 오차도 누적되기 때문입니다. 위치 정보와 속도 데이터 정보 둘 다 활성화 하는것도 잘못된 방법인데, 이는 필터에 중복된 정보를 제공하기 때문입니다.
따라서, 가장 좋은 방법은 다음과 같이 x축 방향 선속도와 y축 방향 선속도, z축 각속도(yaw 각속도)를 사용하는 것입니다.
odom0_config: [false, false, false,
false, false, false,
true, true, false,
false, false, true,
false, false, false]
odom0_differential: false
differential mode에서, 필터는 두 개의 연속된 absolute poses로부터 delta를 계산하고, 이를 속도값으로 변환 후, 그 값을 필터에서 absolute pose가 아닌 속도 입력으로 사용합니다. 이는 두 개의 센서가 각각 absolute variable을 측정하는 경우에 도움이 됩니다. 이런 상황에서는 각각의 센서에서 report되는 값들은 발산하며 의도치 않은 움직임이 발생하게 됩니다. 이 경우에는 단지 하나의 센서만 differential mode를 false로 설정하고, 나머지는 true로 설정하면 부드러운 값의 추정 결과가 나오게 됩니다. 만약 global pose를 측정하는(AMCL이나 GPS등) source가 딱 하나만 있다면, 이 differential 파라미터는 false로 설정해야 합니다.
odom0_differential: false
IMU는 선 가속도, 각 속도, 그리고 accelerometers, gyroscopes, magnetometers를 조합한 absolute orientation 데이터를 제공합니다. 아래 설정에서 볼 수 있듯이, 이 필터는 z축 각 속도와 x축 선 가속도 값을 사용합니다.
imu0: imu
imu0_config: [false, false, false,
false, false, true,
false, false, false,
false, false, true,
true, false, false]
imu0_differential: false
Covariance matrices
process_noise_covariance : 이 파라미터는 필터링 알고리즘의 prediction stage에서 불확실성(uncertainty)를 모델링하기 위해 사용됩니다. 기본적으로, 이는 필터의 결과를 개선하기 위해 사용됩니다. 이 행렬의 대각성분은 pose, 속도, 선 가속도 값을 포함하는 state vector의 분산들입니다. 이 값을 설정하는 것은 필수적이지는 않지만, 튜닝을 잘 하면 결과를 매우 좋게 개선할 수 있습니다. 하지만, 이 분야에 대해 전문가가 아니라면 이를 튜닝하는 것은 쉽지 않습니다. 그래서 가장 좋은 방법은 그냥 다른 값들을 넣어봐서 결과가 좋아지는지 나빠지는지를 실험적으로 확인하는 것입니다. 기본값은 다음과 같습니다.
process_noise_covariance: [0.05, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0.05, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0.06, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0.03, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0.03, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0.06, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0.025, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0.025, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0.04, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0.01, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.01, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.02, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.01, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.01, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.015]
initial_state_covariance : estimate covariance는 현재 상태 추정의 에러를 정의합니다. 이 파라미터는 필터 수렴하는 속도에 영향을 주는 행렬의 초깃값을 설정해줍니다. 여기서는 다음과 같은 규칙이 있습니다. 만약 어떤 변수를 측정중이라면, initial_estimate_covariance의 대각성분 값은 measurement의 covariance보다 커야한다는 것입니다. 예를 들어, 만약 measurement covariance가 1e-6이라면, initial_estimate_covariance의 대각성분 값은 1e-3, 이런 식이어야 한다는 것입니다.
initial_estimate_covariance: [1e-2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 1e-2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1e-2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 1e-2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1e-2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 1e-2, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1e-2, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 1e-2, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 1e-2, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 1e-2, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1e-2, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1e-2, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1e-2, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1e-2, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1e-2]
Test your configuration
다음 명령을 실행하여 필터링을 테스트해봅니다.
| $ roslaunch turtlebot3_gazebo turtlebot3_empty_world.launch $ rosrun rosrun robot_state_publisher robot_state_publisher $ rosrun rosrun ekf_ukf noisy_odom_republisher.py $ roslaunch ekf_ukf plot_odom_drift.launch $ roslaunch ukf_filtering ukf_filtering.launch $ roslaunch turtlebot3_teleop turtlebot3_teleop_key.launch |
그 후, 로봇을 사각형으로 움직여봅니다.
'Study > [ROS] KalmanFilter' 카테고리의 다른 글
| Kalman Filter(4. Particle Filter) (0) | 2021.09.02 |
|---|---|
| Kalman Filters (2. Kalman Filter) (0) | 2021.01.20 |
| Kalman Filters (1. Bayesian Filter) (0) | 2021.01.19 |