이 포스트는 theconstructsim.com의 Kalman Filters 를 참고하였습니다.
이번 포스트에서 다룰 내용은
- Histograms과 가우시안 분포
- 1차원 칼만 필터
- 다차원 칼만 필터
이번 course에서는 turtlebot simulation package를 사용합니다. 아래 링크를 참조하세요
emanual.robotis.com/docs/en/platform/turtlebot3/simulation/
시뮬레이션 모델은 Waffle 모델을 사용합니다.
waffle 모델을 사용하기 위해서는 환경 변수를 추가하거나, bash shell에 해당 명령을 입력하면 됩니다.
$ export TURTLEBOT3_MODEL=waffle
또는, ~/.bashrc 를 수정하여 맨 밑에 export TURTLEBOT3_MODEL=waffle 를 추가합니다.
사용된 ROS버전은 noetic입니다.
ros noetic을 사용할 경우, 외부의 예시를 다운받을 경우 line1의 주석은 항상 python3로 수정해주세요.
#!/usr/bin/env python >> #!/usr/bin/env python3
이번 포스트 관련 이론은 다음 포스트를 참조하세요
soohwan-justin.tistory.com/3?category=941681
3.1. Histograms and Gaussians
이전 포스트에서, 우리는 1차원 discrete grid cells 복도에 있는 로봇을 모델링했으며, RViz를 사용하여 로봇의 위치를 총 합이 1이 되는 값으로 plot했습니다. 이렇게 발생 빈도를 보여주는 막대 plot을 히스토그램이라고 합니다.
우리는 더 작은 grid cells로 나누어서 베이즈 필터를 더 자세하게 만들 수도 있었습니다. 만약 매우 작은 grid cells를 선택했으면, 수천개의 위치에 대해 확률값을 갖는 벡터를 얻게 되었을 것입니다. 이렇게 큰 데이터를 사용하여 베이즈 필터를 빠르게 실행한다면, 실용적이지 못하고, 결국 계산도 할 수 없는 컴퓨팅 부하가 걸리게 될 수도 있습니다.
그렇다면, 필터의 정확도를 높이기 위해서는 어떻게 해야할까요? 먼저, 이전에 사용했던 노이즈가 있는 빛 감지 센서와 노이즈가 있는 오도메트리를 모델링하기 위해 사용했던 불연속 분포의 형태를 떠올려보세요. 이 분포들 가우시안 분포와 비슷하게 생겼습니다.
이제 여기서 나온 아이디어가, 만약 가우시안 분포를 사용하여 동작하는 베이즈 필터를 만든다면 어떻게 될까? 입니다. 이를 위해서는, 우리는 initial state, predict step, correct step을 가우시안에 맞게 조절해야 합니다. 즉, 칼만 필터를 만드는 것입니다.
칼만 필터는 베이즈 필터 중 하나의 예시이며, 다음의 조건을 갖습니다.
- 상태 공간이 연속적입니다
- 초기 상태 확률(initial state probability)가 가우시안 분포를 따릅니다
- motion이 선형적이고, 노이즈는 가우시안 분포를 따릅니다.
- sensor reading의 모델이 선형적이고, 노이즈는 가우시안 분포를 따릅니다.
3.2 One-dimensional Kalman Filter
이전의 포스트에서 belief와 likelihood function을 곱하기 위해서 correct step을 실행했었습니다. 추가적으로, 컨벌루션을 위해서 predict step 또한 실행했었습니다. 칼만 필터에서는, discrete space에서의 확률 벡터를 continous space에서의 확률을 나타내는 가우시안 분포로 대체합니다.
- 칼만 필터가 하나의 변수만을 추정하는 경우에는 1차원이라고 하며, 변수가 많아질 수록 차원이 늘어납니다.
3.3 Filter Initialization
칼만 필터를 초기화하기 위해, 우리는 가우시안 분포를 따르는 initial belief를 설정해야 합니다. 로봇이 state space어디에든 있을 수 있다는 상황을 나타내기 위해, 평균은 상태 공간 내의 무작위 숫자, 분산은 매우 큰 숫자로 초기화됩니다. 예를 들어, state space의 3제곱 같이 큰 수로 합니다. 이렇게 큰 분산은 가우시안 분포를 따르긴 하지만 거의 평평한 분포를 만들게 됩니다.
3.5 Correct Step
측정값 업데이트에서, 우리는 laser ray sensor reading과 이전의 belief를 기반으로 로봇의 위치에 대한 새로운 belief를 업데이트 합니다.
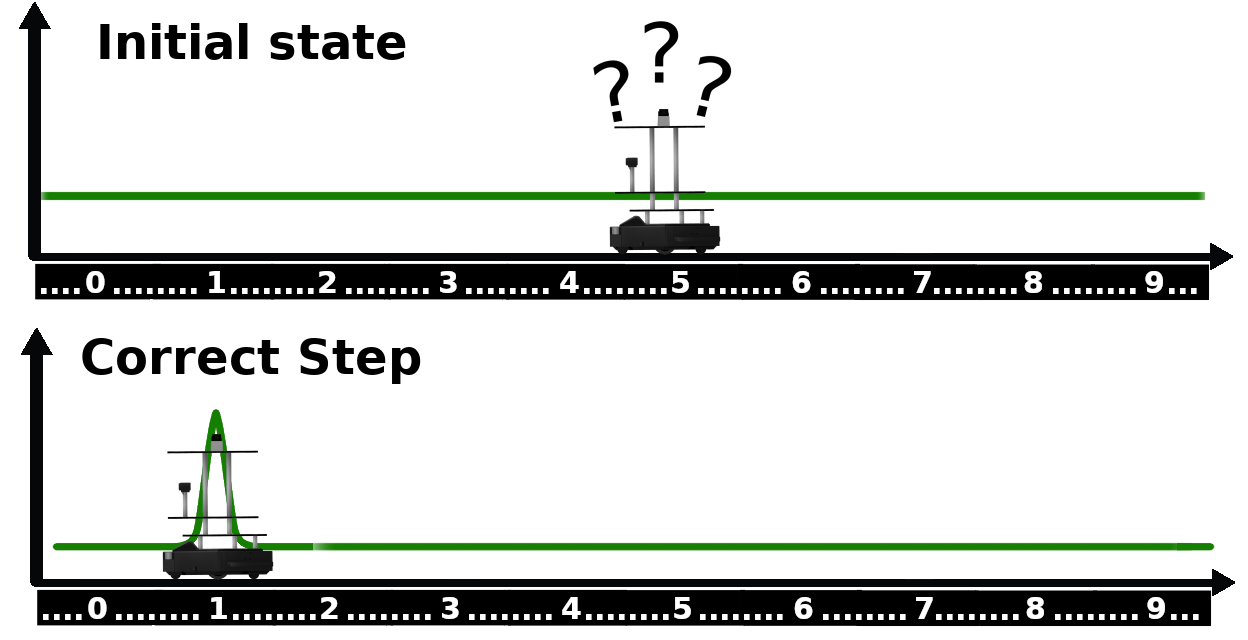
우리는 이런 업데이트를 discrete한 경우에 대해 알아봤는데, 이 때 update step은 likelihood와 이전의 blief의 곱이었습니다.다. continuous state 변수들에도 이와 같은 공식이 적용됩니다.
Likelihood
이전의 예제에서, likelihood를 계산하는 것은 각각의 주어진 측정과 모든 상태의 확률을 찾는 것이 필요했습니다. 연속 확률 분포의 경우, 현재 상태가 주어졌을 때 측정값의 확률은 센서의 측정 모델의 가우시안 분포로부터 주어집니다. 자세한 내용은 가우시안 함수를 참조하세요.
예를 들어, 사용하는 센서가 평균 $\mu$, 분산 $\sigma^2$ 로 모델링 되었고, 센서의 값이 로봇의 위치 x = 5라고 했을 때, 이를 가우시안 함수에 대입하여 이 위치에 대한 확률을 구할 수 있습니다.
Belief
칼만 필터의 첫 번째 사이클에서, initial belief는 평균과 분산의 초기값에 대응됩니다. 그 후의 모든 필터의 반복에서, 추정된 마지막 평균과 분산의 추정은 새로운 측정값을 받을 때 마다 belief로써 사용됩니다. 즉, 새로운 데이터를 받을 때, 기존의 belief로써 업데이트에 사용된다는 것입니다.
그럼, 이제 belief와 likelihood 를 곱해야 하는데, continuous state변수인 이 둘을 곱하려면 어떻게 해야할까요?
Product of two Gaussian distributions
다행이도, 수학자들이 두 개의 가우시안 분포를 곱하는 공식을 다음과 같이 구해뒀습니다. 우리는 이를 그냥 적용해보면 됩니다. 두 분포를 곱한 새로운 분포의 평균이 $\mu'$, 분산이 $\sigma ^2{'}$ 라고 했을 때,
$\mu' = \frac{\sigma^{2}_{1}\mu_2 + \sigma^{2}_{2}\mu_1}{\sigma^{2}_{1} + \sigma^{2}_{2}}$
$\sigma^2{'} = \frac{\sigma^2_1\sigma^2_2}{\sigma^2_1 + \sigma^2_2} = \frac{1}{\frac{1}{\sigma^2_1} + \frac{1}{\sigma^2_2}}$
이 때,
$\mu_1$ = 이전의 평균
$\sigma^2_1$ = 이전의 분산
$\mu_2$ = 측정값의 평균
$\sigma^2_2$ = 측정값의 분산 입니다.
여기서 주목해야할 점은, 각 값들의 상대적인 영향은 그 역수의 값에 의존한다는 점입니다. 그 결과, 확률 밀도 함수의 분산이 작을수록 더 많이 가중됩니다. 분산이 작으면 데이터가 더 정확하다는 것이니, 정확한 데이터에 더 가중치를 두는 것입니다.
위 식을 파이썬 코드로 써보면 더 직관적으로 보입니다.
new_mean = (var1*mean2 + var2*mean1)/(var1+var2)
new_var = 1/(1/var1 + 1/var2)
Predict Step
predict step은 불확실한 로보의 움직임 후, 가능한 로봇의 모든 위치를 추정하는 것입니다. 센서의 측정으로 인해 새로운 가우시안 분포를 얻었다고 해보겠습니다. 이는 현재 로봇의 위치를 나타내는 가장 좋은 추정값입니다. 이제 로봇을 앞으로 움직여서, movement update step을 실행해보겠습니다. 우리는 로봇의 위치를 다음 그림과 같은 가우시안 분포로 나타낼 수 있는데, 로봇의 움직임에 노이즈가 있기 때문에 certainty가 줄어든 분포를 보여줍니다.
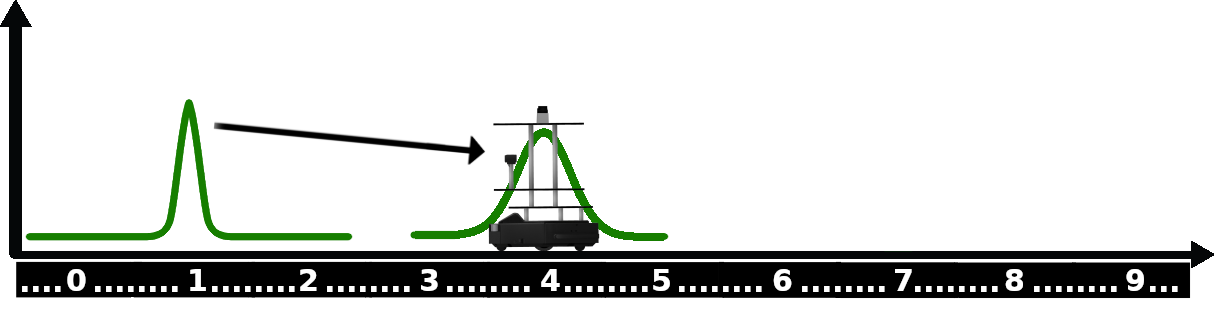
그러면, 그 움직임 이전의 위치 추정에 대한 가우시안 분포와 움직임 이후의 가우시안 분포는 어떻게 조합할까요?
이는 간단하게 두 가우시안 분포의 평균과 분산을 더하면 됩니다.
$\mu' = \mu_1 + \mu_2$
$\sigma^2{'} = \sigma_1^2 + \sigma^2_2$
Multidimensional Kalman Filter
좀 더 간단히 살펴보기 위해, 우리는 로봇이 앞뒤로만 움직이는 공간에서 움직이는 경우에 대해 알아보았습니다. 그러나 우리는 2차원, 3차원, 심지어는 그 이상의 차원에 대해서도 고려를 해봐야 합니다. 이전 단계의 연장선으로, 우리는 x, y좌표와 로봇의 방향 각도를 가진 pose 데이터를 추정할 수도 있습니다. 이번에는 시각화를 위해 2차원의 예시를 사용할 것입니다.
칼만 필터가 1차원 공간에 적용될 때는 간단한 수학적 계산만으로도 충분했지만, 다차원의 경우에는 이를 설명하기 위해 선형대수 가 필요합니다.
Multidimensional Gaussian distributions
지금까지 사용했던 가우시안 분포는 하나의 랜덤변수만을 추정하기 때문에 univariate Gaussian이라고 합니다. 우리는 2개의 변수, $(\mu, \sigma)$에 의해 정의된 1차원 가우시안 분포를 봤습니다.
univariate Gaussian처럼, multivariate normal distribution도 2개의 파라미터로 정의할 수 있습니다.
- 분포의 기댓값을 나타내는 평균 벡터는 𝝁라고 합니다.
- n x n 크기의 공분산 행렬 𝚺는 두 개의 변수가 얼마나 독립적인지, 얼마나 강하게 같이 변하는지를 측정합니다.
보시다시피, n차원 가우시안은 단지 1차원 가우시안을 벡터로 일반화한 것입니다. univariate Gaussian은 평균 $\mu$와 표준편차 $\sigma$로 나타내지만, multivariate Gaussian은 평균 벡터 𝝁와 공분산 행렬 𝚺로나타냅니다.
N 차원 가우시안은 차원 당 하나의 평균을 가지며, 다음과 같이 열벡터로 나타냅니다.
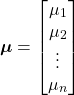
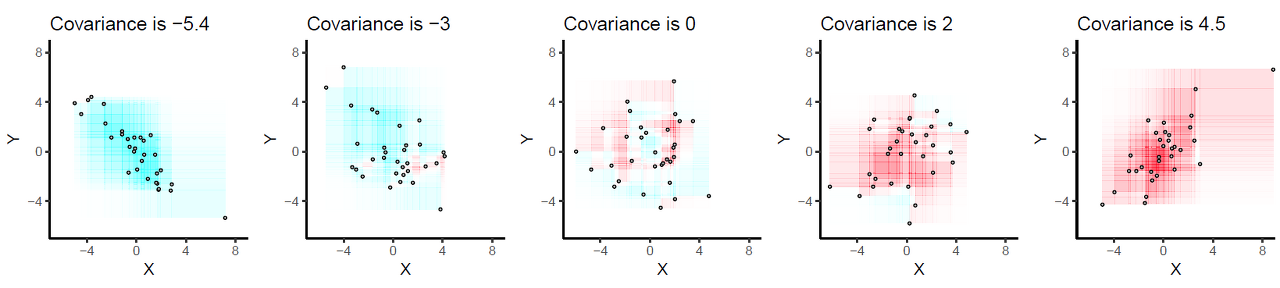
분산에 관해, N차원 Gaussian은 각각의 차원 당 하나의 분산을 가지며, 추가적으로 차원의 각 쌍(pair)마다 하나의 분산을 갖습니다. 공분산은 두 개의 변수가 서로 얼마나 관련이 되어있는지를 측정합니다. 예를 들어, x, y가 있을 때 x가 증가함에따라 y가 증가하거나, x가 증가함에 따라 y가 감소하는 경향이 뚜렷하게 보인다면 공분산이 큰 것이고, 서로 관련이 없다면 공분산이 작은 것입니다.
N차원 Gaussian 또한 공분산 행렬 𝚺로 나타낼 수 있습니다.

행렬의 대각성분들은 각 변수의 분산을 나타내며, 대각성분이 아닌 값들은 가능한 모든 변수들의 쌍에 대한 공분산을 나타냅니다. 공분산 행렬은 d x d 크기를 가지며, d는 추정되는 상태 또는 차원의 크기입니다. 또한, x와 y 또는 y와 x의 공분산이 같기 때문에 공분산 행렬은 대각행렬입니다. 예를 들어, x의 분산이 8, y의 분산이 2이고 둘 사이에 linear correlation이 없다면, 다음과 같이 나타낼 수 있습니다.
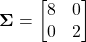
multivariate Gaussian을 통한 slice는 correlations의 시각적인 지표가 될 수 있습니다. 이는 confidence ellipse라고 하는 것을 보여줍니다. correlation이 작을수록, 타원은 더 원에 가까워집니다. 만약 타원이 날씬한 모양이라면, 두 개의 변수가 강하게 correlated 되어있다는 것을 의미합니다. correlation의 값의 부호는 타원의 방향을 나타냅니다.
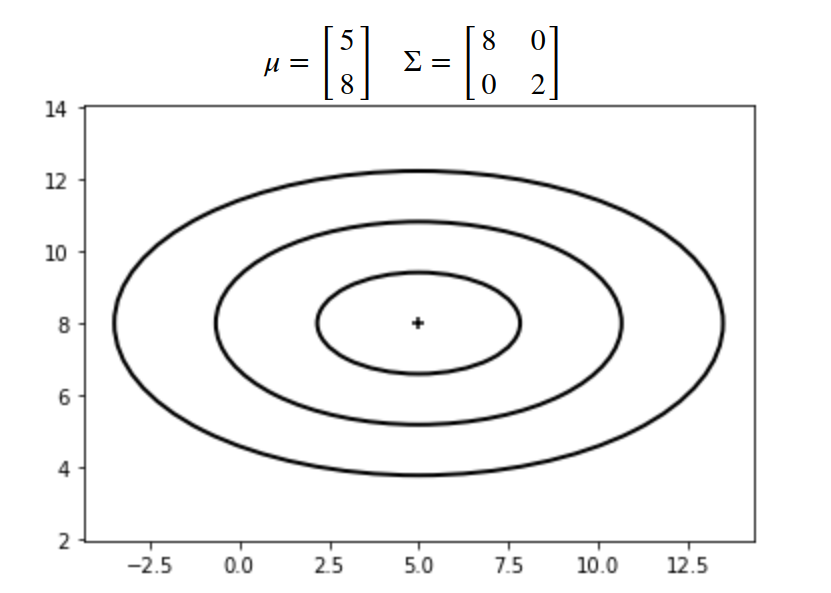
위 공분산을 3d 그래프로 plot하면 다음과 같습니다.
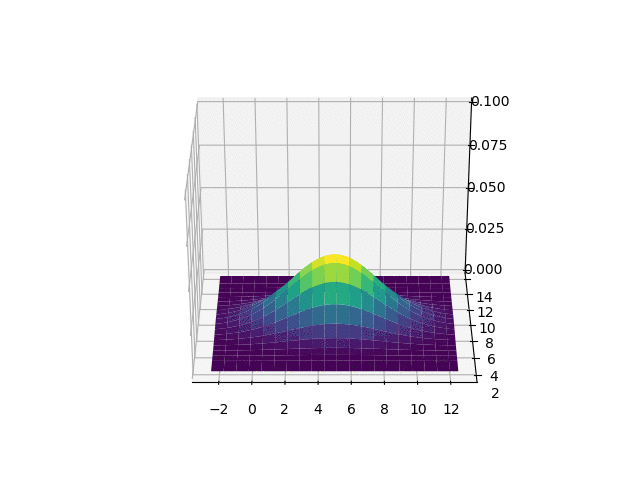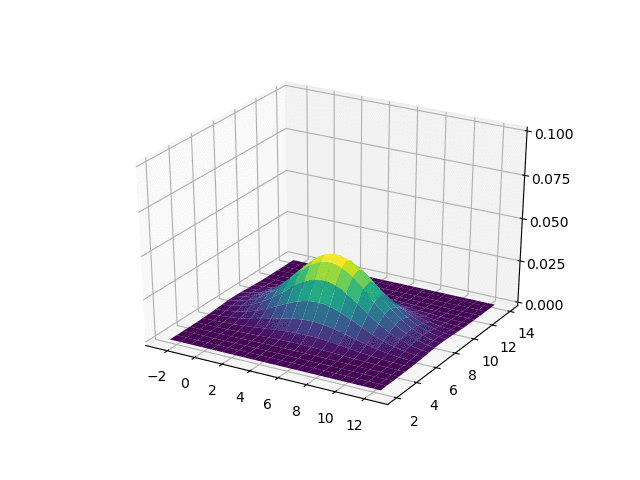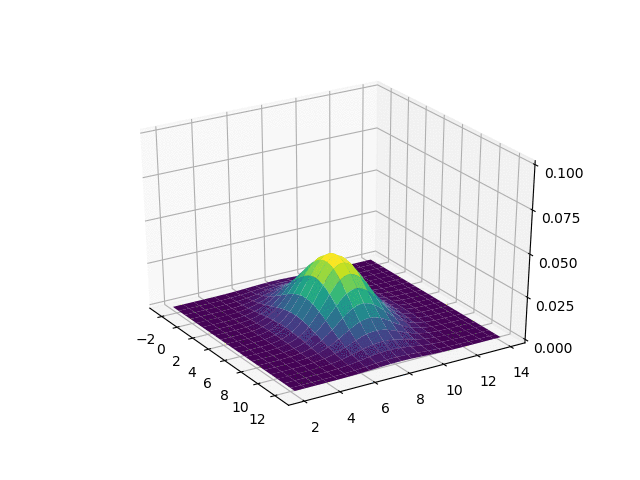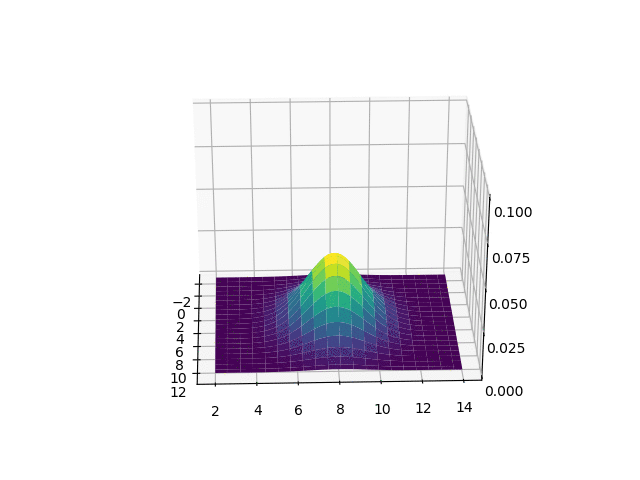
2D localization 문제에서, X와 Y축은 2D 지도에서의 (x, y)좌표를 나타내며, Z축은 가능한 위치의 조합에 대한 확률을 나타냅니다. 위 그림에서 가장 높은 지점은 평균인 (5, 8)인데, 이는 로봇이 다른 곳 보다 x, y = (5, 8) 주변에 있을 확률이 높다는 것을 의미합니다.
Multiplying Multidimensional Gaussians
이전의 포스트에서 보았듯이, 두 개의 가우시안의 곱은 그 곱의 결과인 가우시안 추정을 더 정확하게 해주는 속성을 갖고있습니다. 이 속성은 고차원 가우시안 분포에서도 마찬가지입니다.
평균 벡터의 곱은 다음과 같습니다.
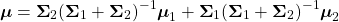
두 가우시안 함수의 곱의 공분산 행렬은 다음과 같습니다.

Multidimensional Kalman Filter Equations
우리는 칼만 필터 알고리즘은 prediction step, update step으로 구성되어있다는 것을 알았습니다. 이제는 각각의 step에 대한 일반화된 형태의 다차원 칼만 필터 방정식을 알아보겠습니다.
Prediction Step
predict step의 첫 번째 방정식은 새로운 평균 벡터 $\overline{\bf x}$ 를 계산하는 것입니다.
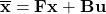
이 함수들은 상태 과도 행렬(state transistion matrix)인 $\bf{F}$와 현재 평균 벡터 $\bf x$ 로부터 새로운 상태인 $\overline{\bf x}$를 구합니다. $\bf B$는 control matrix라고 하며, $\bf u$는 control vector라고 합니다. 대부분의 응용 분야에서 control input이 없을 수도 있으며, 이 경우에는 $\bf B$와 $\bf u$가 생략될 수 있습니다.
state transistion matrix 또는 그냥 transistion matrix라고도 하는 $\bf F$는 칼만 필터에서 아주 중요한 부분입니다. $\bf F$ 상태 변수가 어떤 시점으로 부터 다른 시점으로 변하는 방정식을 나타냅니다. 행렬 형태의 transistion matrix는 현재 드론의 상태(위치, 방향, 속도, 가속도)가 다음 타임 스텝의 드론의 상태에 어떻게 영향을 미칠지를 나타냅니다.
위의 식을 보면, 좌항은 output state $\overline{\bf x}$이고, 우항에는 state transistion matrix와 각각 가능한 input이 있는 것을 볼 수 있습니다. transistion matrix의 각각의 요소들은 어떤 input이 output state에 영향을 주는지, 어떻게 영향을 주는지를 보여줍니다. 만약 어떤 input이 output state에 영향을 주지 않는다면, 그에 해당되는 행렬 요소는 0이 될 것입니다. motion model의 state transistion matrix을 정의하는 방법에 대한 예제는 나중에 따로 설명하겠습니다.
위에 나타난 state transistion matrix는 transfer function, state transistion model, process model, systems dynamics matrix, fundamental matrix라고도 합니다. 또한, 아래의 table과 같이 $\bf F$대신 $\bf A$로 나타내기도 합니다.

predict step에서 두 번째 방정식은 새로운 variance-covariance matrix $\overline{\bf P}$를 계산하는 것입니다. 이전에, 우리는 대문자 시그마 $\bf{\Sigma}$ 를 사용하여 공분산 행렬을 나타냈지만, 이제는 $\bf P$를 사용할 것입니다. 칼만 필터는 공분산 행렬로 $\bf P$를 사용하며, 이제 우리는 이 규약에 익숙해져야 합니다.
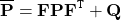
위 식은 $\bf{\overline{P}}$를 계산하기 위해서는 $\bf FPF^\tt{T}$를 계산해야 한다는 것을 의미하며, 이는 단지 상태 변수들간의 correlation을 $\bf{\overline{P}}$로 통합하고, 정규 분포를 따르는 노이즈 공분산 $\bf Q$를 더하는 대수적인 방법입니다. 위의 식들을 외울 필요는 없고, 무슨 의미인지만 알아두도록 하세요.
Correct Step
이번 스텝에서는, 우리는 중간 값을 계산하고, 이 값들을 다음 단계에서 평균과 분산을 계산하는데에 사용합니다.
먼저, innovation또는 measurement residual이라고 하는 $\bf y$를 계산할 것입니다.
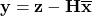
$\bf H$는 meausrement matrix라고 합니다. 이는 현재 상태를 measurement mean vector $\bf z$와 관련시킵니다. 즉, 이 값의 차이(residual)는 실제 측정과 예측된 측정값의 차이를 수량화 합니다.
다음으로, 우리는 innovation(또는 residual) covariance matrix $\bf S$를 계산해야 합니다. 이는 $\mathbf{H\overline{P}H^\tt T} $ 를 포함하며, state prediction covariance는 measurement space에서 표현되고, measurement noise covariance matrix $\bf R$를 더합니다. 즉,
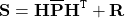
다음으로, 칼만 이득이라고 하는 $\bf K$를 계산할 것입니다. 이는 state prediction과 measurement update의 업데이트에 얼마나 큰 가중치가 적용되어야 하는가를 의미합니다.
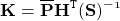
마지막으로, 칼만 이득과 residual은 새로운 state mean과 state variance를 계산하기 위해 사용됩니다.
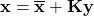
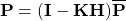
'Study > [ROS] KalmanFilter' 카테고리의 다른 글
| Kalman Filter(4. Particle Filter) (0) | 2021.09.02 |
|---|---|
| Kalman Filters(3. Extended Kalman Filter and Unscented Kalman Filter) (0) | 2021.08.30 |
| Kalman Filters (1. Bayesian Filter) (0) | 2021.01.19 |